Решение:

Выполним чертеж:

H

M

C (4, -2)

B (-3, -1)

A (1, 7)

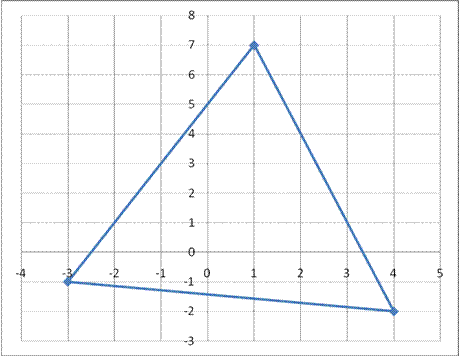
Для нахождения уравнений сторон треугольника воспользуемся формулой уравнения прямой, проходящей через две точки А₁ (x₁ , y₁ ) и
А₂ (x₂ , y₂ ):

подставив поочередно в формулу (1) попарно координаты точек А и В , В и С , А и С .

Уравнение прямой, проходящей через точки А (1, 7) и В (-3, -1):

Уравнение прямой, проходящей через точки В (-3, -1) b C ( 4,-2) :

Уравнение прямой, проходящей через точки А (1, 7) и C ( 4,-2):

Для определения уравнения медианы ВМ предварительно вычислим координаты точки М, воспользовавшись формулами нахождения координат середины отрезка А₁ А₂ (А₁ (x₁ , y₁ ) и А₂ (x₂ , y₂ )):

где х₁ , у₁ – координаты точки А (1, 7);

х₂ , у₂ – координаты точки С (4, -2).

Координаты точки М:

Точка М имеет координаты х = 2,5 и у = 2,5 , т. е. М (2,5; 2,5).

Для нахождения уравнения медианы ВМ воспользуемся формулой (1), подставив в нее координаты точек В (-3, -1) и М (2,5; 2,5) .

Уравнение медианы ВМ: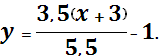

Для определения уравнения высоты СН воспользуемся формулой уравнения прямой, проходящей через данную точку М₁ ( x ₁ , y ₁ ) перпендикулярно к данной прямой y = ax + b :

подставив в нее координаты точки С( 4,-2 ) и данные из уравнения прямой АВ Получим:

Уравнение высоты СН:

3. Вычисление определителей.

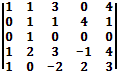
Решение:

Используя алгебраические преобразования, получим в первом столбце в четвертой и пятой строке нули. Для этого от элементов четвертой строки отнимем элементы первой строки и полученный результат запишем на место элементов четвертой строки матрицы. От элементов пятой строки отнимем элементы первой строки и полученный результат запишем на место элементов пятой строки матрицы. Получим:

Разложим определитель матрицы по элементам первого столбца, имеем:

Такой прием называется сведением определителя более высокого порядка к определителю более низкого порядка.

Во второй строке последнего определителя все элементы строки, кроме элемента первого столбца, равны нулю. Поэтому удобно разложить определитель матрицы по элементам второй строки. В результате получим следующий результат.