Контрольная работа: Функции и их производные
подставляем найденные выражения в уравнение, получаем: 
, что и требовалось доказать.
№5
Найти 
если 
Вычислить если 
.
Воспользуемся формулами нахождения производных для функций, заданных параметрически
№ 6.
Функции задана неявно уравнением
Вычислить:
а) 
Вычисления проводим по формуле
б)
№ 7.
На графике функции y=ln2x взята точка А. Касательная к графику в точке А наклонена к оси ОХ под углом, тангенс которого равен ј. Найти абсциссу точки А.
Из геометрического смысла производной 
имеем
№ 8.
Найти dy, если у=х6 . Вычислить значение dy, если
Для 
имеем
№ 9.
Дана функция 
и точки 
и 
Вычислить Дz и dz при переходе из точки М0 в точку М1 . Приращение функции Дz равно
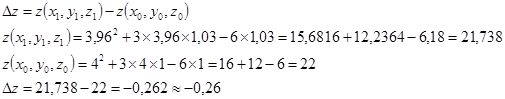
Дифференциал функции dz равен