Контрольная работа: Функции и их производные

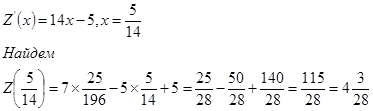
На границах отрезка

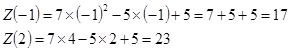
Сравниваем все найденные значения функции

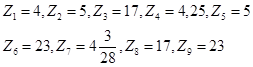
видим, что наибольшее значение достигается в точке (2;-1) и равно 23, а наименьшее равно 4 и достигается в точке (0;0).

Ответ: 23;4.

№ 12.

Провести полное исследование функции и начертить ее график.

1. Найдем область определения функции .

Функция непериодична.

2. Установим наличие симметрии относительно оси OY или начала координат по четности или нечетности функции , симметрии нет.

3. Определим «поведение функции в бесконечности»

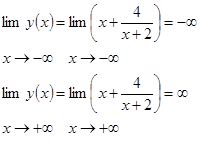
4. Точка разрыва х=-2

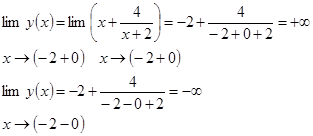
5. найдем пересечение кривой с осями координат

т.А (0;2)

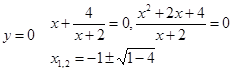
Корней нет, нет пересечения с осью OY.

6. Найдем точки максимума и минимума

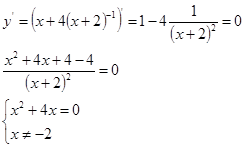
в точке производная меняет знак с <-> на <+>, следовательно имеем минимум, в точке производная меняет знак с <+> на <->, имеем максимум.

При первая производная отрицательна, следовательно, функция убывает, при производная положительна, функция в этих промежутках возрастает.

7. Найдем точки перегиба

, точек перегиба нет. При вогнутость вверх, при , вогнутость вниз.

8. Найдем горизонтальные и наклонные асимптоты в виде , где