Контрольная работа: Генерирование коррелированных случайных процессов в среде LabVIEW

Изображенный фильтр описывается системной (передаточной) функцией

K(z^-1 ) = b₀ + b₁ z^-1 + b₂ z^-2 + … + b_k z^-k .

Передаточная функция в стандартной форме, полученная из системной функции умножением числителя и знаменателя на z^k , имеет вид:

K(z) = (b₀ z^k + b₁ z^{k - !} + … + b_k )/z^k .

Недостаток СС-фильтра: увеличение порядка фильтра с увеличением количества отсчетов корреляционной функции. Если корреляционная функция имеет бесконечную протяженность, то для сокращения порядка фильтра ее искусственно ограничивают по времени, пренебрегая малыми значениями корреляционной функции. Это приводит к возникновению методической ошибки моделирования.

Авторегрессионный метод Существенная экономия машинных ресурсов и возможность моделирования случайных процессов с корреляционной функцией бесконечной протяженности достигается при использовании авторегрессионного метода. Авторегрессионный метод предполагает использование рекурсивных фильтров с системной функцией

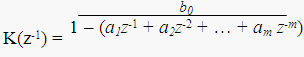
где m – порядок фильтра.

Как следует из вида системной функции, выходной процесс авторегрессионного фильтра (АР-фильтра) связан с входным процессом рекуррентным соотношением

y(nT) =b₀ x(nT) + a₁ y(nT – T) + a₂ y(nT – 2T) + … + a_m y(nT – mT).

Корреляционная функция определяется коэффициентами a_i . Непосредственно по этому выражению нельзя найти корреляционную функцию, зная коэффициенты a_i , как это было сделано по выражению (2). Для выявления качественного влияния коэффициентов на форму корреляционной функции воспользуемся ее связью с импульсной характеристикой фильтра. Рассмотрим сначала АР-фильтр первого порядка (рис. 7).

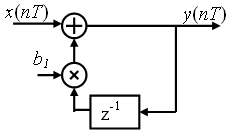
Рис. 7

Его передаточная функция в стандартной форме

K(z) =.

Импульсная характеристика определяется как обратное Z – преобразование от передаточной функции:

g[n] = b₀ a₁ ⁿ ( 4)

Диапазон возможных значений коэффициента a₁ ограничивается устойчивостью фильтра. Для устойчивости АР-фильтра требуется, чтобы полюса его передаточной функции находились внутри окружности единичного радиуса.

Полюс находится приравниванием нулю знаменателя передаточной функции:

z – a₁ =0.

Полюс

z₁ = a₁ ,

и требование устойчивости фильтра

| a₁ | < 1 или -1 < a₁ < 1.

При положительном a₁ импульсная характеристика, как следует из ( 4), является монотонно спадающей функцией, и корреляционная функция тоже будет монотонно спадающей. При отрицательном а₁ импульсная характеристика становится колебательной, и корреляционная функция будет колебательной затухающей с периодом колебаний равным двум интервалам дискретизации.

Рассмотрим, как будет изменяться АЧХ фильтра, а следовательно, и энергетический спектр ( 1) генерируемой последовательности, при изменении а₁ . Комплексная частотная характеристика получается из передаточной функции К(z) подстановкой z = e^jωΔt . Амплитудно-частотная характеристика

К(ω) = |b₀ e^jωΔt /(e^jωΔt – a₁ )| = b₀ /|e^jωΔt – a₁ |.

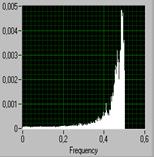
Она обратно пропорциональна модулю разности векторов e^jωΔt и a₁ . Как видно из рис. 8 а), при положительном a₁ модуль разности векторов будет изменяться от наименьшего значения при ω = 0 до наибольшего значения при ωΔt = π. Значит, АЧХ, а следовательно, и энергетический спектр случайной последовательности, будет иметь подъем в области низких частот. При отрицательных a₁ , наоборот, подъем будет в области верхних частот.

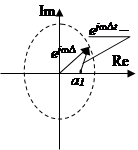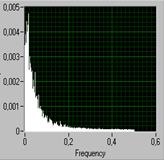а)	б)	в)
Рис. 8

На рис. 8, б) показан энергетический спектр процесса на выходе фильтра при a₁ = 0,8; а на рис. 8, в) – при a₁ = - 0,8.