Контрольная работа: Графы

Цикл – конечная цепь, у которой начальная и конечная вершина совпадают.

Граф называется связанным, если любые его две вершины можно соединить цепью. Граф сильно связан, если для его двух любых вершин х _i ≠х _j существует путь, идущий из х _i и х _j .

Граф, который не является связанным, может быть разбит на конечное число связных графов, называемых компонентами, или частями.

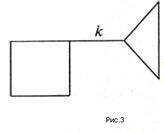
Ребро графа G называется мостом, если граф, полученный из G путем удаления этого ребра, имеет больше компонент связности, чем граф G .

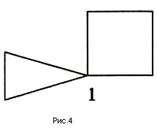
Точкой сочленения графа называется вершина, удаление которой приводит к увеличению числа его компонент связности.

На рисунке 3 ребро к – мост, а на рисунке 4 вершина 1 – точка сочленения.

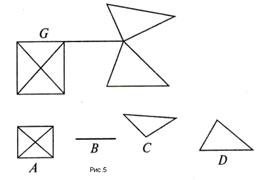
Неразделимым называется связный граф, не имеющий точек сочленения.

Блоком графа называют максимальный неразделимый подграф.

На рисунке 5 приведен граф Gи его блоки А, В, С и D.

Дерево это конечный, связный, не ориентированный граф, не имеющий циклов.

Характеристическое свойство деревьев состоит в том, что любые две вершины дерева соединены единственной цепью.

Теория деревьев была, в основном, разработана Кирхгофом. Он применил ее для решения систем линейных уравнений, описывающих работу электрических цепей.

Кирхгоф Густав (1824–1887) немецкий физик, механик, математик.

Развитие теории графов (деревьев) связано с именем немецкого химика Кели, который успешно применил ее для решения задач органической химии (для изучения изомеров углеводородов с заданным числом атомов).

Совокупность деревьев называется лесом.

Если все вершины графа принадлежат дереву, то он называется покрывающим. Пусть дано множество вершин графа. Одну из вершин, например х₁ , примем за начальную, которую назовем корнем дерева. Из этой вершины проводим ребра к остальным вершинам х₂ , х₃ и т.д.

Простейшее дерево состоит из двух вершин, соединенных ребром.

Если добавить ребро, то добавляется и вершина. Таким образом, дерево с п вершинами имеет n-1 ребро. Дерево имеет корень в вершине В_р еслисуществует путь от х₁ , к каждой из вершин. Ребра графа, принадлежащие дереву, называют ветвями, остальные ребра называют хордами.

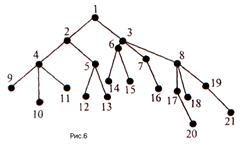
Граф называется планарным, если он может быть изображен на плоскости таким образом, что его ребра будут пересекаться только в планарных вершинах (рис. 6).

Дерево, являющееся подграфом графа G , называется покрывающим граф G , если оно содержит все его вершины.

Пусть имеется х₁ , х₂ ,…, х _n вершин и u ₁ , u ₂ …, u_m дуг, их содержащих. Матрицей смежности S порядка п называется матрица, состоящая из чисел S ., равных сумме чисел ориентированных ребер, идущих из х в х. (или чисел неориентированных ребер, соединяющих эти вершины). Если дуга отсутствует, то S_r = 0.

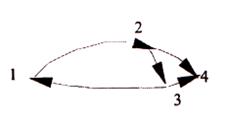
Матрица смежности для ориентированного и неориентированного графа, вообще говоря, имеет разный вид. Запишем матрицу смежности 5, для ориентированного графа, изображенного на рисунке 7:

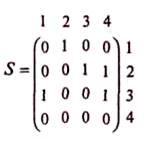
Матрицей инциденции Т размера m x n называется матрица, состоящая из чисел:

		tij =

Запишем матрицу инциденции для графа, изображенного на рисунке 7:

Операции над графами

Объединением двух, или более графов G₁ , UG ₂ U … UG_n называется граф, у которого множество вершин и множество дуг объединены (рис. 8).