Контрольная работа: Графы

Задача о максимальном потоке

Рассмотрим двухполюсную сеть S =( N , U ) с одним входом (источником) s є N и выходом (стоком) t є N , дуги сети ( i , j ) є U имеют ограниченную пропускную способность с _ij . Задача о максимальном потоке заключается в поиске таких потоков j _ij по дугам ( i , j ) если, что результирующий поток из источника в сток является максимальным.

Математическая модель задачи о максимальном потоке выглядит следующим образом:

найти такие значения j _{ij ,} при которых

V=åj_sj =åj_sj Þmax;

jj

при ограничениях:

0<= j_ij <=c_ij

åj_ij -åj_ij =0 i є N i¹s i¹t.

jj

Для решения этой задачи может быть использован метод построения увеличивающих цепей.

Построение максимального потока

На практике часто возникают задачи определения максимального количества товара, которое может быть перевезено от производителя потребителю. Аналогичными являются задачи определения максимальной пропускной способности системы автомагистралей, определения максимального количества нефти или газа, передаваемых по трубопроводам, информации, пропускаемой по компьютерной или телефонной сети. Формально эти проблемы сводятся к задаче построения максимального потока в сети. Для их решения необходимо ввести несколько понятий.

Пусть задана сеть S=(N, U) с множеством вершин N и множеством дуг U.

Определение. Дуга u є U, соединяющая вершины i є N, j є N сети S, называется допустимой дугой , если она обладает одним из следующих свойств:

1) направление дуги совпадает с направлением потока, и значение потока по этой дуге меньше ее пропускной способности:

u=(i, j), j(u)<c(u);

2) направление дуги противоположного направлению потока, и величина потока отлична от нуля:

u=(j, i), j(u)>0.

Дуги, обладающие первым свойством, называют увеличивающими ; дуги, обладающие вторым свойством, – уменьшающими .

Определение . Увеличивающей цепью, соединяющей вход и выход сети, называется простая цепь, все дуги которой являются допустимыми.

Пример 1. Построим увеличивающую цепь для сети S=(N, U), представленной на рисунке 15.

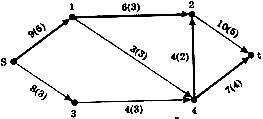Над каждой дугой указана ее пропускная способность, в скобках – поток по этой дуге.

Цепь (s, 1, 2, 4, t) является увеличивающей, так как все дуги – допустимые:

· дуга (s, 1) – увеличивающая, так как она проходит по направлению потока, и поток по ней меньше ее пропускной способности: 6 < 9;

· дуга (1,2) – также увеличивающая дуга: 3 < 6;

· дуга (2,4) – уменьшающая, так как она проходит против потока и поток по ней 2 > 0;

· дуга (4, t) – увеличивающая: 4 < 7.

Пример 2. Построим максимальный поток для сети, представленной на рис. 4.16.