Контрольная работа: Интегральные преобразования. Радиоуправление

где функция, сопряженная по Гильберту сигналу

Особенностью определенного комплексного сигнала заключается в том, что его спектральная плотность:

(14)

и содержит только положительные частоты, тогда

Значит, если узкополосному сигналу соответствует спектральная плотность , модуль которой изображен на Рис 3 штриховой линией, то сигналу соответствует спектральная плотность , модуль которой изображен сплошной линией.

- спектральная плотность исходного (физического ) сигнала

Комплексный сигнал, определяемый выражениями (13 ) и (14) называется аналитическим сигналом.

Рис 3. Соотношения между спектрами физического и аналитических сигналов.

5 Характеристики аналитического сигнала

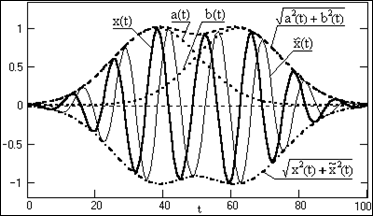
Огибающая и мгновенная фаза сигналов. Допустим, что имеем зарегистрированный радиоимпульсный сигнал x(t) с несущей частотой _o , который содержит определенную информацию, заключенную в огибающей сигнала u(t) и его фазе (t):

x(t) = u(t) cos (_o t+(t)). (.15)

Требуется выделить информационные составляющие сигнала

Запишем выражение (16.2.1) в другой форме:

x(t) = a(t)×cos(_o t) + b(t)×sin(_o t), (16)

где функции a(t) и b(t) называются низкочастотными квадратурными составляющими сигнала x(t):

a(t) = u(t) cos t, b(t) = u(t) sin t.

u(t) =, tg (t) = b(t)/a(t).

С использованием преобразования Гильберта из сигнала x(t) можно сформировать аналитически сопряженный сигнал (t). Математическую форму сигнала (t) получим из выражения (16) с учетом свойства модуляции преобразования Гильберта:

(t) = a(t)×sin(_о t) – b(t)×cos(_o t).

z(t) = x(t) + j×(t).

Квадрат модуля сигнала z(t):

|z(t)|² = x² (t)+² (t) = a² (t)[cos² (_ t)+sin² (_o t)] + b² (t)[cos² (_ t)+sin² (_o t)] = u² (t).

Отсюда, огибающая u(t) и мгновенная фаза (t) сигнала x(t):

u(t) =. (17)

t_o t+(t) = arctg[(t)/x(t)]. (18)

Наглядно эти характеристики можно увидеть на Рис 4