Рисунок 2 – график зависимости у=f(x)

Таблица 5 – Сравнительный анализ заданных и принятых значений Y

X	1.01	1.51	2.02	2.51	3.01	3.49	3.98	4.48	4.99	5.49
Y	5.02	5.92	7.14	8.32	9.02	9.58	11.06	11.96	12.78	13.98
Y1	5.06	6.05	7.05	8.02	9.01	9.95	10.92	11.91	12.91	13.90
E	-0.04	-0.13	0.09	0.30	0.01	-0.37	0.14	0.05	-0.13	0.08

Вывод: На основе собранных статистических данных, представленных в таблице находим экономическую модель – принятая гипотеза имеет степенную зависимость и выражается уравнением

y = 1.9733 x + 3.0667

Экономическое прогнозирование на основе уравнения данной зависимости отличается достоверностью в области начальных значений параметра X– величина ε принимает малые значения и неточностью в долгосрочном периоде – в области конечных значений параметра X.

Задача №3

7. Связь между тремя отраслями представлена матрицей прямых затрат А. Спрос (конечный продукт) задан вектором X. Найти валовой выпуск продукции отраслей Х. Описать используемые формулы, представить распечатку со значениями и с формулами.

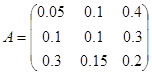
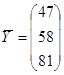
Решение

Данная задача связана с определением объема производства каждой из N отраслей, чтобы удовлетворить все потребности в продукции данной отрасли. При этом каждая отрасль выступает и как производитель некоторой продукции и как потребитель своей и произведенной другими отраслями продукции. Задача межотраслевого баланса – отыскание такого вектора валового выпуска X, который при известной матрице прямых затрат обеспечивает заданный вектор конечного продукта Y.

Матричное решение данной задачи:

X = ( E - A )^-1 Y . [2]

Из существующих в пакете Excel функций для работы с матрицами при решении данной задачи будем использовать следующие:

1. МОБР – нахождение обратной матрицы;

2. МУМНОЖ – умножение матриц;

3. МОПРЕД – нахождение определителя матрицы;

Также при решении данной задачи использовали сочетание клавиш:

F2 CTRL + SHIFT + ENTER – для получения на экране всех значений результата.

Расчетные формулы для решения данной задачи показаны в таблице 7.

Результат решения показан в таблице 6.

Таблица 6 – Расчетные формулы

Затраты	Выпуск (потребление)		Конечный		Валовый
(отрасли)	отрасль А	отрасль B	отрасль C	продукт	выпуск
отрасль А	0.05	0.1	0.4	47	=МУМНОЖ (F12:H14; E3:E5)
отрасль B	0.1	0.1	0.3	58	=МУМНОЖ (F12:H14; E3:E5)
отрасль C	0.3	0.15	0.2	81	=МУМНОЖ (F12:H14; E3:E5)
Решение
Е =	1	0	0
	0	1	0
	0	0	1
Е-А =	=B8‑B3	=C8‑C3	=D8‑D3	(Е-А)-1 =	=МОБР (B12:D14)	=МОБР (B12:D14)	=МОБР (B12:D14)
	=B9‑B4	=C9‑C4	=D9‑D4		=МОБР (B12:D14)	=МОБР (B12:D14)	=МОБР (B12:D14)
	=B10‑B5	=C10‑C5	=D10‑D5		=МОБР (B12:D14)	=МОБР (B12:D14)	=МОБР (B12:D14)
Det (E-A)=	=МОПРЕД (B12:D14)

Таблица 7 – Результат решения

Затраты	Выпуск (потребление)			Конечный	Валовый
(отрасли)	отрасль А	отрасль B	отрасль C	продукт	выпуск
отрасль А	0.1	0.1	0.4	47	140
отрасль B	0.1	0.1	0.3	58	140
отрасль C	0.3	0.15	0.2	81	180
Решение
Е =	1	0	0
	0	1	0
	0	0	1
Е-А =	1	-0.1	-0.4	(Е-А)-1 =	1.322880941	0.27438	0.76433
	-0.1	0.9	-0.3		0.333170015	1.25429	0.63694
	-0.3	-0.2	0.8		0.558549731	0.33807	1.65605
Det (E-A)=	0.51025

Вывод: Для удовлетворения спроса на продукцию отрасли А величиной 47 д.е., отрасли В – 58 д.е. и отрасли С – 81 д.е. необходимо произвести продукции отрасли А на сумму 140 д.е., отрасли В на сумму 140 д.е., отрасли С – на сумму 180 д.е.

Задача №4

Вариант 15 Коммерческий магазин хочет закупить овощи А и В. Количество овощей, закупочные цены и цены, по которым магазин продает овощи, приведены в таблице 8.

Таблица 8

Овощи	Цены		Количество овощей
	Закупка	Реализация
А	1,6	2,4	60
В	1,7	2,2	70

Как выгоднее вложить деньги, если общая сумма, которой располагается магазин в данное время, составляет 180 д.е., причем овощей А нужно приобрести не менее 10 тонн.

Решение

Решение данной задачи состоит из трех основных этапов:

1. составление математической модели (формализация задачи);

Обозначим величину прибыли от овоща А как А, а величину прибыли от обоща В как В, тогда получим, что прибыль от продажи овоща А составляет (2,4–1,6) А, соответственно овоща В – (2,2–1,7) В. Суммарная прибыль магазина от продажи овощей составит (2,4–1,6) А+(2,2–1,7) В=0,8А+0,5В.

Тогда целевая функция имеет вид Z =0,8А – 0,5В

суммарная прибыль должна быть наибольшей (максимальной).