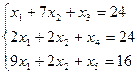Контрольная работа: Исследование зависимости между объемом производства, капитальными вложениями и выполнением норм
1) х1+7х2≥24 (0;3,43) (24;0)
2) 2х1+2х2≥24 (0;12) (12;0)
3) 9х1+2х2≥16 (0:8) (1,78;0)
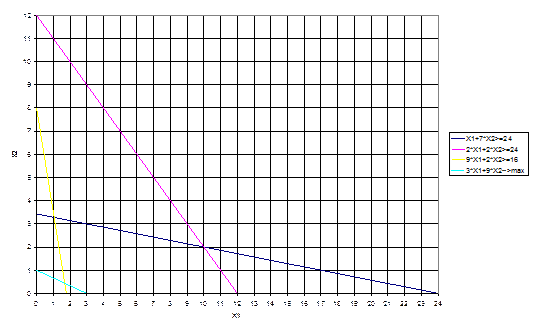
Однако нам необходимо найти такую точку, в которой достигался бы max целевой функции.
Оптимальную производственную программу можно найти двумя способами:
1) путем перебора его вершин
Находим координаты вершин многоугольника ABCDE и подставляя в целевую функцию находим ее значение.
А: А (0; 0) Z(A) =3×0+9×0=0
В: В (0; 3,43) Z(B) = 3×0+9×3,43=30,87
D: D (1,78; 0) Z(B) = 3×1,78+9×8=5,38
С: – это пересечение первого и второго уравнений
;
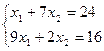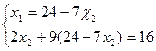;216 -63x 2 +2x 2 =16; x 2 =1,04.
С (1,04; 3,28) Z(C) = 3×1,04+9×3,28=32,64
Находим max значение целевой функции. Оно находится в точке
С (1,04; 3,28). Таким образом max прибыль составит 32,68у.д.е. при выпуске продукта Р в количестве 1,04 у.е. и R – 3,28 у.е.
2) геометрическим способом
Целевая функция геометрически изображается с помощью прямой уровня, т.е. прямой на которой Z=3X1 +9X2 – принимает постоянное значение.
Если С – произвольная const, то уравнение прямой имеет вид
3X1 +9X2 =С
При изменении const С получаем различные прямые, параллельные друг другу. При увеличении С прямая уровня перемещается в направлении наискорейшего возрастания функции Z, т.е. в направлении ее градиента. Вектор градиента 
Точкой min Z будет точка первого касания линии уровня с допустимым многоугольником. Точкой max – точка отрыва линии уровня от допустимого многоугольника. Эти точки чаще всего совпадают с некоторыми вершинами допустимого многоугольника, хотя их может быть и бесчисленное множество, если линия уровня Z параллельна одной из сторон допустимого многоугольника. Это точка С (1,04; 3,28) Z=32,68 у.д.е.
Решим задачу с помощью симплекс-таблиц.
Пусть необходимо найти оптимальный план производства двух видов продукции P и R.
1. Построим оптимизационную модель:
F(X)=3X1 +9X2 →max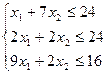 
2. Преобразуем задачу в приведенную каноническую форму. Для этого введем дополнительные переменные X3 , X4 и X5 .
F(X)=3X1 +9X2 →max 