Контрольная работа: Измерение частоты и интервалов времени
![]() и
и
Суммарные погрешности (абсолютная и относительная) измерения периода определяются выражениями:
![]() , [c]
, [c]
 , [%]
, [%]
Повышение эффективности обработки сигналов при оценке частотно-временных параметров
Выбор и оптимизацию алгоритмов обработки данных при оценке частотно-временных параметров исследуемых сигналов выполняют при разработке и построении самых различных радиотехнических систем и приборов, работающих на этих принципах. Наиболее распространенным методом построения аппаратуры и выводы о предельных значениях статистических оценок среднего значения частотно-временных параметров в случае отсутствия априорных данных об исследуемом сигнале, является метод обнаружения и оценки значений неизвестных параметров по максимуму функции правдоподобия, который реализуется в корреляционных и многоканальных устройствах. Трудности, связанные с реализацией таких устройств обеспечивающих потенциальные точностные характеристики, привели к тому, что на практике нашли широкое распространение классические одноканальные цифровые устройства обработки сигналов (цифровые измерители среднего значения мгновенной частоты частотомеры), для которых исследование механизма возникновения и снижения погрешностей при оценке частотно-временных параметров является актуальной задачей исследования. Возможности повышения эффективности обработки сигналов при оценке частотно-временных параметров можно получить, исследуя распространенную модель аддитивной смеси гармонического сигнала и узкополосного детерминированного или случайного процесса:
![]() ,
,
где Um , ![]() 0 и
0 и ![]() 0 - амплитуда, угловая частота и начальная фаза сигнала, а A ( t ) и θ( t) - огибающая и фаза случайного процесса ξ( t) ; U( t),
0 - амплитуда, угловая частота и начальная фаза сигнала, а A ( t ) и θ( t) - огибающая и фаза случайного процесса ξ( t) ; U( t), ![]() ( t) иΦ( t) - огибающая, случайная фаза и полная фаза аддитивной смеси, представляющая собой случайный нестационарный процесс.
( t) иΦ( t) - огибающая, случайная фаза и полная фаза аддитивной смеси, представляющая собой случайный нестационарный процесс.
Одной из исследуемых функцией, представляющей практический интерес, является мгновенная частота, связанная с полной фазой известным соотношением:
ω ( t )= d Φ ( t )/ dt =ω0 + ![]() ( t) ,
( t) ,
где![]() ( t)=
( t)=![]() ( t) - случайная частота, определяемая через производную случайной фазы аддитивной смеси и характеризующая скорость ее изменения.
( t) - случайная частота, определяемая через производную случайной фазы аддитивной смеси и характеризующая скорость ее изменения.
Оценка математического ожидания случайного процесса ![]() (t) на интервале времени усреднения Т в общем виде может быть выполнена по формуле [2]:
(t) на интервале времени усреднения Т в общем виде может быть выполнена по формуле [2]:
|
 ,
,
где g ( t ) – весовая функция оператора сглаживания, удовлетворяющая условию несмещенности оценки:
|

Среднее значение мгновенной частоты, вычисляемое классическими цифровыми частотомерами, определяется по приращению полной фазы сигнала на интервале времени усреднения T = tk - t н , то есть используется информация о значениях полной фазы в начале Φ( t н ) и конце Φ( tk ) измерительного интервала с приращением, равным:
![]()
или относительно середины измерительного интервала:
|
Из приведенных аналитических выражений следует, что классический измеритель среднего значения мгновенной частоты реализует операцию дифференцирования фазы сигнала, а (3) является дифференциально-разностным уравнением, для которого существует интегральная форма, являющаяся оператором текущего сглаживания:
|

совпадающим с (1) при ![]() и осуществляет выборку усредненных значений мгновенной частоты с равномерным шагом, кратным времени измерения.
и осуществляет выборку усредненных значений мгновенной частоты с равномерным шагом, кратным времени измерения.
Использование весовой обработки в соответствии с выражением (1), позволяет существенно повысить точность и помехоустойчивость устройств, работа которых основана на использовании формулы (4). Как показано в [2], оптимизация весовой обработки позволяет получать практически потенциальные оценки среднего значения мгновенной частоты при стационарных флуктуациях случайной фазы исследуемого сигнала.
Эффективность весовой обработки при переходе к цифровому измерению среднего значения мгновенной частоты снижается по сравнению с обобщенным алгоритмом (1). При цифровых измерениях с весовой обработкой результатов промежуточных отсчетов искомое значение среднего значения мгновенной частоты определяется в дискретные моменты времени, а оценка среднего значения мгновенной частоты при циклических измерениях производится с интервалом дискретности, пропорциональным времени усреднения, то есть на выходе измерителя формируется функция m1 (ω(кT)) , где к - число циклов усреднения.
Выражение (3) для оценки среднего значения мгновенной частоты при цифровом усреднении классическим измерителем преобразуется к виду:
 ,
,
а интегральная форма (4) может быть представлена суммой:
|
 ,
,
где ![]() - интервал квантования по времени, n - количество усредняемых промежуточных временных интервалов. Оператор текущего сглаживания (1) с произвольной весовой функцией g ( t ) преобразуется в аналитическое выражение:
- интервал квантования по времени, n - количество усредняемых промежуточных временных интервалов. Оператор текущего сглаживания (1) с произвольной весовой функцией g ( t ) преобразуется в аналитическое выражение:
|

где усредненное значение результирующей оценки мгновенной частоты на интервале времени измерения образуется суммой промежуточных отсчетов средних значений мгновенной частоты взятых с соответствующим весом. Усредненное значение мгновенной частоты по дискретной выборке при этих условиях можно представить как взвешенную сумму разности отсчетов промежуточных значений полной фазы аддитивной смеси на интервале времени измерения:
|

где ![]() - приращение полной фазы исследуемого сигнала на временном интервале
- приращение полной фазы исследуемого сигнала на временном интервале ![]() t в i -м промежуточном измерении. В соответствии с выражением (7), усредненное значение мгновенной частоты определяется через суммирование приращений полной фазы результирующего сигнала
t в i -м промежуточном измерении. В соответствии с выражением (7), усредненное значение мгновенной частоты определяется через суммирование приращений полной фазы результирующего сигнала ![]()
В связи с квантованием по времени возникает задача выбора интервала квантования случайного нестационарного процесса, обеспечивающего минимальное увеличение дисперсии оценки среднего значения мгновенной частоты гармонического сигнала. Решение этой задачи проведем для дискретной весовой функции Бартлетта, обладающей высокой эффективностью сглаживания флуктуационных помех [3]. Оптимизировать интервал квантования можно как в спектральной области на основе частотных характеристик усредняющих устройств, зависящих от используемых весовых функций и спектральных особенностей воздействующих помех или временным методом, исследовав погрешности оценки (7). Последнее в данном случае представляется наиболее доступным, поэтому, учитывая условие несмещенности оценки (2) и дискретную весовую функцию Бартлетта, определим дисперсию оценки (7) по общим правилам для суммы зависимых случайных величин [4]:
|

где ![]() - дисперсия фазовых флуктуаций усредняемой реализации; R ( i
- дисперсия фазовых флуктуаций усредняемой реализации; R ( i![]() t ) - значение нормированной корреляционной функции фазовых флуктуаций, разделенных временным интервалом t = i
t ) - значение нормированной корреляционной функции фазовых флуктуаций, разделенных временным интервалом t = i ![]() t . После преобразований, формула (8) приводится к виду:
t . После преобразований, формула (8) приводится к виду:
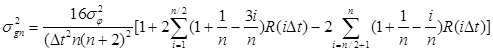
|