Контрольная работа: Изучение упругого и неупругого ударов шаров

9)

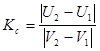
Если при соударении потеря кинетической энергии отсутствует (K_с = 1), то удар называется абсолютно упругим, а при K_с = 0 абсолютно неупругим. Если же 0 < K_с < 1, то удар является не вполне упругим.

Применительно к соударяющимся шарам, один из которых покоится, формулу (4) можно записать так:

10) , а для абсолютно неупругого удара .

Скорости шаров до и после удара можно определить по формулам:

11) ; 12) ; 13)

где l – расстояние от точки подвеса до центра тяжести шаров (l = 470 ± 10 мм.), a₀ – угол бросания правого шара, a₁ и a₂ – углы отскока соответствующих шаров.

Расчётная часть

№	ti ´10-6	Dti ´10-6	(Dti ´10-6 )2	a1i	Da1i		a2i	Da2i
1	76	-14	196	2°	-0,5°	0,25°	12°	-0,2°	0,04°
2	103	13	169	2°	-0,5°	0,25°	13°	0,8°	0,64°
3	96	6	36	3°	0,5°	0,25°	11°	-1,2°	1,44°
4	93	3	9	2,5°	0°	0°	13°	0,8°	0,64°
5	82	-8	64	3°	0,5°	0,25°	12°	-0,2°	0,04°
90			2,5°			12,2°

После работы с установкой имеем значение следующих величин: (угол бросания правого шара) a₀ = 15°; (массы правого и левого шаров соответственно) m₁ = 112,2 ´ 10^-3 кг, m₂ = 112,1 ´ 10^-3 кг; (длина бифилярных подвесов обоих шаров) l = 470 ´ 10^-3 м; (погрешность значения длин бифилярных подвесов) Dl = 0,01 м; (цена деления микросекундометра) c_t = 10^-6 ; (цена деления градусных шкал) c_a = 0,25°.

При известном среднем арифметическом значении времени найдём погрешность измерения данной величины:

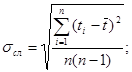
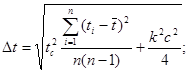
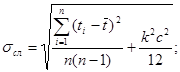
с.

с.

При известных значениях и найдём погрешность их измерения (в радианах, при p = 3,14):

рад.

рад.

рад.

рад.

при D_сл » 0;рад.

при s_сл » 0; s_{a 0} = s_с ; ;

рад.

Теперь найдём скорости данных шаров до соударения (V₁ , V₂ ) и их скорости после взаимодействия (U₁ , U₂ ). При этом (скорость левого шара) V₂ = 0 т. к. он покоиться до удара. Значения остальных скоростей находят из следующих формул (через l, a и g):

м/с² ; м/с² ; м/с² ;

Найдём погрешности вычисления данных скоростей.

м/с.

м/с.