Контрольная работа: Коллинеарность и компланарность векторов. Канонические уравнения прямой

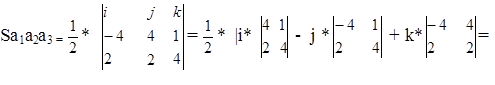
= |i*(4*4 - 1*2) - j*((-4)*4 - 2*1)+k*((-4)*2 - 2*4)= |14i + 18j - 16k|=

=√14² +18² -16² =√264=*16,25=8,125

h==11,94

Задача 6. Расстояние от точки М₀ до плоскости, проходящей через три точки

.

М₁ (1; 2; 0 ) М₂ (3; 0; -3 ) М₃ (5; 2; 6 ) М₀ (-13; -8; 16 )

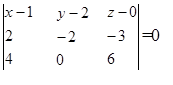
(х-1) * ((-2)*6 - 0*(-3)) - (у-2)*(2*6 - 4*(-3)) + (z- 0)*(2*0 - 4*(-2))=0

(-12)*(х - 1) - 24*(у - 2) + 8*(z- 0) = 0

(-3)*(х - 1) - 6*(у - 2) + 2*(z- 0)=0

-3х - 6у + 2Z+ 15 = 0

d==

Задача 7. Уравнение плоскости, проходящей через точку А перпендикулярно вектору .

А (-3; -1; 7 ) B (0; 2; -6 ) C (2; 3; -5 )

={2; 1; 1}

2*(х + 3) + 1*(у + 1) + 1*(z- 7)=0

2х + у + z= 0

Задача 8. Угол между плоскостями

2у + z- 9=0

х - у + 2z- 1=0

п₁ ={0; 2; 1 }

п2={1; -1; 2 }

cosφ===90

Задача 9. Координаты точки А, равноудаленной от точек В и С.

А (х; 0; 0 ) B (4; 5; -2 ) C (2; 3; 4 )

АВ===

АС===

=