Контрольная работа: Коллинеарность и компланарность векторов. Канонические уравнения прямой

Задача 1. Коллинеарность векторов

а = { 2; -1; 6 } в = { -1; 3; 8 }

c₁ =5a – 2b = {5*2 – 2*(-1); 5*(-1) – 2*3; 5*6-2*8 } = {12; -11; 14 }

с₂ =2а – 5в = {2*2 – 5*(-1); 2*(-1) – 5*3; 2*6-5*8 } = {9; -17; -28 }

≠ ≠-

12/9 ≠ 11/17 ≠ -14/28

Ответ: не коллинеарны.

Задача 2. Косинус угла между векторами АВ и АС

А (3; 3; -1 ) B (5; 1; -2 ) C (4; 1; -3 )

= {2; -2; -1 } || ==

= {1; -2; -2 } || = =

cos (ˆ) = =

Задача 3. Площадь параллелограмма построенного на векторах а и в.

а=5p-qb=p+q |p|=5 |q|=3 (pˆq) = 5

S=|5p- q|*|p+ q|=|5p*p + 5p*q - q*p - q*q|=|5p*q+ p*q| =6*|p*q|=6|p|*|q|*sin(pˆq)=

=6*5*3*sin5

sin5= 90*=45

Задача 4. Компланарность векторов а, в, с.

а = { 1; -1; 4 } в = { 1; 0; 3 } с = { 1; -3; 8 }

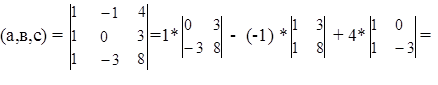
1*(0*8 - 3*(-3)) - (-1)*(1*8 - 1*3)+4(1*(-3) - 1*0)=9 + 5 - 12=2

2≠0 - не компланарны.

Задача 5. Объем тетраэдра с вершинами в точках А₁ А₂ А₃ А₄ и его высоту, опущенную из вершины А₄ на грань А₁ А₂ А₃ .

А₁ = { 0; -3; 1 } А₂ = { -4; 1; 2 } А₃ = { 2; -1; 5 } А₄ = { 3; 1; -4 }

₌ { -4; 4; 1 }

₌ { 2; 2; 4 }

₌ { 3; 4; -5 }

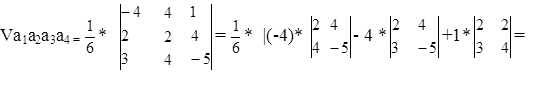
=* |(-4)*(2*(-5) - 4*4) - 4*(2*(-5) - 3*4) + 1*(2*4 - 3*2)=

--> ЧИТАТЬ ПОЛНОСТЬЮ <--