Контрольная работа: Логический анализ E-структур с помощью графов

Пути такого типа называются в упорядоченных структурах максимальными путями. В произвольных E-структурах их может быть больше двух, они могут самым причудливым образом пересекаться друг с другом, но все они обладают двумя главными свойствами:

1) из совокупности этих путей можно полностью восстановить CT-замыкание E-структуры, используя только правило транзитивности, и

2) ни одна связь в этих путях не может быть получена из других связей с помощью правила транзитивности.

Определение 2. Диаграммой Хассе E-структуры называется граф, содержащий только связи, включенные в максимальные пути и не содержащий никаких связей, полученных по правилу транзитивности. Диаграмма Хассе E-структуры является ее инвариантом.

Таким образом, мы можем любую E-структуру представить не только с помощью CT‑замыкания, но и с помощью диаграммы Хассе. При этом структура становится более наглядной. Попробуем оценить, сколько лишних связей мы используем, если представляем ее в виде CT-замыкания. Для простоты представим, что наша E-структура содержит два максимальных пути, и каждый из этих путей содержит N базовых терминов. Тогда общее число связей в диаграмме Хассе этой структуры равно 2(N-1). В CT-замыкании той же самой структуры будет содержаться уже N(N-1) связей. Определим, сколько связей будет «сэкономлено» при использовании диаграммы Хассе. Обозначим число таких "лишних" связей буквой K. Тогда

K = N(N-1) -2(N-1) = -3N + 2.

Выражение -3N + 2 является полиномом второй степени от N. Это означает, что при увеличении числа N количество «сэкономленных» связей K возрастает в квадратичной зависимости. Так, при N = 4 число связей в диаграмме Хассе и в CT‑замыкании будет равно соответственно 6 и 12, но если N = 10, то соотношение будет уже другим: 18 и 90. Разница и соответственно «экономия» будут уже существенными.

У диаграммы Хассе имеется еще одно интересное свойство, которое можно практически использовать при анализе E-структур и соответственно при анализе моделируемых с их помощью рассуждений. Это свойство определяется следующей теоремой. Пусть имеется некоторая E-структура G, заданная определенными суждениями (посылками). Граф структуры G, который получается после применения правила контрапозиции (правила C) ко всем посылкам обозначим G^C , а диаграмму Хассе этой структуры (если мы ее каким-то способом сумели построить) – G^H . Тогда соблюдается следующее соотношение:

Теорема 1. Для любых E-структур соблюдается G^H ÍG^C .

Это означает, что после того, как будут построены контрапозиции исходных посылок, в полученном графе будут в наличии все дуги диаграммы Хассе. Хотя не исключено, что при этом в графе будут присутствовать и лишние для диаграммы Хассе дуги, которые мы можем легко распознать и удалить.

Но наша «экономия» лишних связей на этом не заканчивается. Можно, оказывается, любую E-структуру представить числом связей, в два раза меньшим, чем число связей в диаграмме Хассе. Обратите внимание, что в диаграмме Хассе все связи «ходят парами»: суждение и его контрапозиция. А почему бы нам каждую такую пару не представить всего одним суждением? Ведь все равно изъятое суждение мы получим, применив к оставшемуся суждению правило контрапозиции.

Этот инвариант, составленный из половины суждений диаграммы Хассе, назван минимальным множеством посылок E-структуры. Почему минимальным? А потому что исходная E-структура может содержать посылки, которые на самом деле логически следуют из остальных посылок. Если эту E-структуру дополнить всеми следствиями, получаемыми с помощью правила C, а потом преобразовать полученную систему в диаграмму Хассе, то мы, сравнивая исходные посылки с суждениями диаграммы Хассе, сможем найти «лишние» (т.е. выведенные из других посылок) посылки среди исходных.

Логическая система, в которой ни одна посылка не является следствием каких-либо других посылок, называется независимой. В качестве примера рассмотрим, является ли независимой E-структура, заданная следующими посылками:

A®; ®; C®; C®.

Строим граф с посылками (рисунок 3) и к каждой посылке достраиваем контрапозицию (рисунок 2, 3)

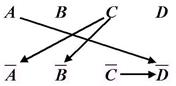
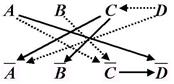
Рис. 3Рис. 4

Присмотревшись внимательно к графу на рисунке 4, мы увидим, что дуга A® соединяет литералы, между которыми имеется путь A®®. Отсюда следует, что система не независима и посылка A® является следствием других посылок (C® и ®). Чтобы из графа на рисунке 4 получить диаграмму Хассе данной структуры, нужно изъять из этого графа дугу A® и ее контрапозицию D®.

Использование свойств диаграммы Хассе в E-структурах позволяет, во-первых, определить структурные сходства и различия в них, во-вторых, оценить независимость исходных посылок и, в-третьих, существенно уменьшить объем памяти для их представления на электронном носителе.