Контрольная работа: Математические методы экономических исследований

где 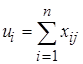– общее промышленное и производственное потребление, далее:

,

где vj - непроизводственное потребление и накопление.

В принципе формула (3.1) представляет математическую модель межотраслевого баланса в сфере потребления.

Отрасль можно анализировать не только с точки зрения распределения ее продукции, но и с точки зрения затрат на производство в данной отрасли. Пусть в этом случае в i-ой отрасли имеются затраты на заработную плату zi , кроме этого в балансе необходимо предусмотреть доход Di (i = 1, 2, ..., n). Тогда баланс по затратам будет иметь для i-ой отрасли следующий вид:

, i = 1, 2, ..., n,

т.е. стоимость продукции i-ой отрасли равна стоимости продукции, затраченной от всех n отраслей, плюс заработная плата и доход от реализации продукции этой отрасли.

Введем определение коэффициента прямых затрат в виде соотношения:

, или .

Подставляя последнее соотношение в (3.1), получим:

,

или в векторной форме:

w = Aw + v. (3.2)

Пусть себестоимость производства одной единицы продукции j-ой отрасли будет равна cj . Тогда общие народнохозяйственные расходы выражаются соотношением:

.

Ставится следующая задача оптимизации плана , когда:

,

а линейная форма L обращается в минимум.

Таким образом, приходим к так называемой статической модели межотраслевого баланса.

Очевидно, что условиям задачи может удовлетворять множество наборов значений xi (i = 1, 2, ..., n). Каждый такой набор носит название допустимого решения (стратегии, управления, плана). То решение, которое доставляет минимум целевой функции (линейной форме L) называется оптимальным.

Поиск решения задачи межотраслевого баланса путем обращения матрицы (I - A) в различных аспектах был предложен Леонтьевым В., и в научных кругах задача с матрицей (I - A) называется задачей Леонтьева.

Матрица A получила название матрицы Леонтьева. Матрица (I-A)^-1 называется матрицей коэффициентов полных затрат. Основной результат межотраслевого анализа может быть сформулирован в виде матричного равенства:

w = (I - A)^-1 v . (3.3)

Матрица A называется продуктивной, если матрица (положительная). Нормой матрицы A назовем максимум сумм элементов ее столбцов. Она обозначается ||A||. Можно доказать, что если A положительная матрица и , причем хотя бы для одного столбца сумма его элементов строго меньше 1, то A будет продуктивной матрицей.

Тема 4. Задачи на смеси

1. Постановка задачи на смеси.

2. Графический метод решения.

3. Общий алгоритм решения задач линейного программирования.

Краткое содержание темы

Задачи на смеси являются одним из показательных классов задач по линейному программированию в области планово-экономических исследований. На примере таких задач могут быть рассмотрены основные методы решения задач линейного программирования как одного из крупных разделов математических методов экономических исследований.

Классическая задача на смеси ставится следующим образом. Из различных видов сырья объемом соответственно b₁ , b₂ ,..., b_m-1 , b_m можно изготовить n видов продукции. Пусть цена единицы j-го вида продукции будет c_j и для изготовления единицы j-го продукта требуется затратить i-ый вид сырья в количестве a_ij единиц. Возникает вопрос, какие виды продукции и в каком количестве нужно производить, чтобы получить наибольшую выручку?