Контрольная работа: Математические методы в экономике
Задание 1. Графоаналитический метод решения задач линейного программирования
Постановка задачи: Необходимо найти решение задачи, состоящей в определении максимального значения функции F=c1 x1 +c2 x2 , где переменные xj ≥0 (j=1;2) – планируемое количество единиц j-й продукции, а сj – прибыль на единицу j-й продукции при условиях ai 1 x1 +ai 2 x2 ≤bi (i=1,…,k), xj ≥0 (j=1,2).
Решение
1. Заменяем ограничения-неравенства на ограничения-равенства (привести задачу к каноническому виду).
2. Построим прямые, соответствующие полученным уравнениям.
3. Определить полуплоскости, соответствующие заданным неравенствам в системе ограничений.
4. Поиск области допустимых решений задачи.
5. Построить градиент функции цели: grad F=(F’x 1 ; F’x 2 ).
6. Построить прямую нулевого уровня c1 x1 +c2 x2 =0, (эта прямая перпендикулярна градиенту).
7. Переместить эту прямую в направлении градиента, в результате чего будет найдена точка (точки), в которой целевая функция принимает максимальное значение, или же установлена неограниченность функции на множестве планов.
8. Определить координаты точки максимума функции и вычислить значение целевой функции в этой точке.
Система ограничений:
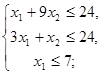
Целевая функция ![]() .
.
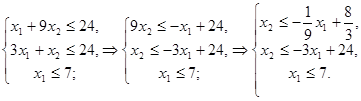 (1)
(1)
Построим прямые, ограничивающие многоугольник допустимых решений:
|
|
|