Контрольная работа: Математичне програмування
Розв’язок
Побудова математичної моделі. Нехай xij — кількість продукції, що перевозиться з і-го пункту виробництва до j-го споживача 
. Оскільки 
, то задачу треба закрити, тобто збалансувати (зрівняти) поставки й потреби:
У нашому випадку робиться це введенням фіктивного постачальника, оскільки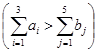 
. З уведенням фіктивного споживача транспортній таблиці додатково заявляється n робочих клітинок.
Ціни, додатковим клітинкам, щоб фіктивний стовбець був нейтральним щодо оптимального вибору планових перевезень, призначаються усі рівні нулю.
Занесемо вихідні дані у таблицю.
| В1 | В2 | В3 | В4 | В5 | В6 | Запаси | |
| А1 | 5 | 2 | 3 | 6 | 1 | 0 | 150 |
| А2 | 1 | 1 | 4 | 4 | 2 | 0 | 320 |
| А3 | 4 | 1 | 2 | 3 | 5 | 0 | 400 |
| Потреби | 100 | 120 | 100 | 200 | 300 | 50 |
Забезпечивши закритість розв'язуваної задачі, розпочинаємо будувати математичну модель даної задачі:
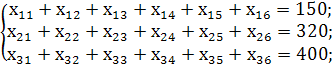
Економічний зміст записаних обмежень полягає в тому, що весь вантаж потрібно перевезти по пунктах повністю.
Аналогічні обмеження можна записати відносно замовників: вантаж, що може надходити до споживача від чотирьох баз, має повністю задовольняти його попит. Математично це записується так:
Загальні витрати, пов’язані з транспортуванням продукції, визначаються як сума добутків обсягів перевезеної продукції на вартості транспортування од. продукції до відповідного замовника і за умовою задачі мають бути мінімальними. Тому формально це можна записати так:
minZ=5x11+2x12+3x13+6x14+1x15+0x16+1x21+1x22+4x23+4x24+2x25+0x26+4x31+1x32+2x33+3x34+ +5x35+0x36.
Загалом математична модель сформульованої задачі має вигляд:
minZ=5x11+2x12+3x13+6x14+1x15+0x16+1x21+1x22+4x23+4x24+2x25+0x26+4x31+1x32+2x33+3x34+ +5x35+0x36.
за умов:
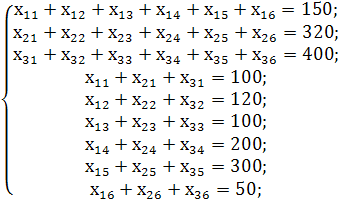
Запишемо умови задачі у вигляді транспортної таблиці та складемо її перший опорний план у цій таблиці методом «північно-західного кута».
| Ai | Bj | ui | |||||
| b1 = 100 | b2 = 120 | b3 = 100 | b4=200 | b5=300 | b6=50 | ||
| а1 = 150 |
5 100 |
2 [-] 50 | 3 | 6 |
1 [+] | 0 | u1 = 0 |
| а2 = 320 | 1 |
1 [+] 70 |
4 К-во Просмотров: 345
Бесплатно скачать Контрольная работа: Математичне програмування
| ||||