Контрольная работа: Метод Гаусса для решения систем линейных уравнений

1. Система линейных алгебраических уравнений

1.1 Понятие системы линейных алгебраических уравнений

Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких переменных. Системой линейных алгебраических уравнений (далее – СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:

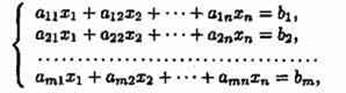
где числа a_ij называются коэффициентами системы, числа b_i – свободными членами, a_ij и b_i (i=1,…, m; b=1,…, n) представляют собой некоторые известные числа, а x₁ ,…, x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент. Подлежат нахождению числа x_n . Такую систему удобно записывать в компактной матричной форме: AX=B. Здесь А – матрица коэффициентов системы, называемая основной матрицей;

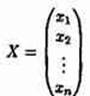– вектор-столбец из неизвестных xj.

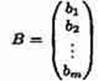– вектор-столбец из свободных членов bi.

Произведение матриц А*Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).

Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов

1.2 Решение системы линейных алгебраических уравнений

Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений системы обращается в верное равенство.

Решением системы называется n значений неизвестных х1=c1, x2=c2,…, xn=cn, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца

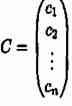
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: перестановка местами двух уравнений системы, перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений, умножение обеих частей какого-либо уравнения системы на отличное от нуля число.

Система линейных уравнений называется однородной, если все свободные члены равны нулю:

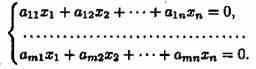
Однородная система всегда совместна, так как x1=x2=x3=…=xn=0 является решением системы. Это решение называется нулевым или тривиальным.

2. Метод исключения Гаусса

2.1 Сущность метода исключения Гаусса

Классическим методом решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных – метод Гаусса (его еще называют методом гауссовых исключений). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Процесс решения по методу Гаусса состоит из двух этапов: прямой и обратный ходы.

1. Прямой ход.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--