Контрольная работа: Метод построения трехмерной модели формы клетки по данным светового трансмиссионного микроскопа
Рис. 2. Нахождение Q(z). Обозначения:
.
.
.
.
.
.
Алгоритм нахождения Q(z) (рис. 2).
1. Относительно полярной системы координат клетки составить интерполяционную формулу функции, описывающей контур сечения клетки, перпендикулярный оси z, по формуле 1. 1 п. 2.
2. 
.
3. 
, так как 
– параллелограмм.
4. 
.
5. Интерполируем функцию Q(z). При этом независимая переменной будет z (по пункту 3), а зависимой величина 
. Тогда интерполяционная формула Ньютона будет иметь вид:
.
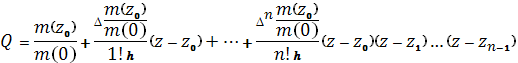Где 
, 
, 
, 
, 
.
6. Определить Q(z) по пунктам 1 - 4 для 20 клеток.
7. Для каждого коэффициента 
построить дискретную функцию 
, где N – это номер клетки в ряду исследованных. Данную функцию можно задать таблицей соответствия значений области определения и области значения. Затем найдем 
(среднее значение коэффициента).
8. Определим между какими клетками лежит найденное среднее значение. Та клетка из найденной пары, к значению которой лежит ближе , считается средней по данному коэффициенту .
9. После того как были найдены средние клетки по всем коэффициентам (их 20, см. пункт 4) находим частоты с которыми клетки становились средними по формуле 
, где p – частота, с – число коэффициентов по которым клетка становилась средней, С=20.
10. Выбираем клетку с наибольшей частотой p, ее функция Q(z) и считается функцией данного клеточного типа.
1.3 Построение трехмерной модели формы клетки
1. На гистологическом срезе, перпендикулярном z, на глаз выбираем 20 наиболее крупных клеток и выбираем среди них среднюю по алгоритмам из пунктов 1. 1 и 1. 2, однако уже не относительно координаты z, а относительно координаты y. Выбранная клетка с высокой вероятностью представляет собой среднее сечение (сечение клетки плоскостью, которая задается уравнением 
). Принимаем, что граница среднего сечения описывается функцией в полярных координатах 
).
2. Из уравнений 
и имеем общий вид уравнения поверхности клетки в трехмерных координатах:
.
2. Прейдем от прямоугольно-полярной системы к прямоугольной, тогда уравнение поверхности клетки будет иметь вид:
.
4. Введем полученное уравнение в программу Maple 8 ввиде:
> with(plots): implicitplot3d((x^2+y^2)^0.5-Q(z)*r(cos(arctan(y/x))=0,
x=-r(-0.5*π)..r(0.5*π), y=-r(π)..r(0), z=-R(-0.5*π)..R(0.5*π),
scaling=UNCONSTRAINED);.