Контрольная работа: Метод скінчених різниць в обчислювальній математиці

Одним з найбільш простих і досить ефективних методів

оцінки похибки й уточнення отриманих результатів є правило Рунге. Для оцінки похибки за правилом Рунге порівнюють наближені розв’язки, отримані при різних кроках сітки. При цьому використовується наступне припущення: глобальна похибка методу порядку p у точці х_i подається у вигляді

.

За формулою Рунге

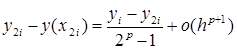
Таким чином, із точністю до (величина більш високого порядку малості) при h→0 похибка методу має вигляд:

де y_i – наближене значення, отримане в точці з кроком h; y_2i – із кроком h/2; p - порядок методу; y(x_2i ) - точний розв’язок задачі.

Метод прогнозу і корекц ії

Підправивши схему Эйлера , одержимо схему прогнозу

,

де наближене значення . Цю формулу використовувати не можна ,оскільки схема прогнозу нестійка . Тому використовує-мо схему корекції

Оцінюючи похибки прогнозу і корекції, одержимо

- похибка корекції,

- похибка прогнозу .

Істинне значення лежить між прогнозом і корекцією .На будь-якому кроці можна оцінити точність рішення . При заданому =0,0000001, наприклад, .

Віднімаючи з співвідношення , маємо

.

Уточнюємо розв’язання, виходячи з формули :

Ця формула завершає схеми прогнозу і корекції .

Метод кінцевих різниць для розв ’ яза ння лінійних крайових задач

Маємо відрізок [a,b]. Потрібно знайти розв’язок лінійного диференціального рівняння другого порядку

,

що задовольняє такі крайові умови:

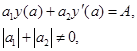
Виберемо рівномірну сітку: x = a + ih, i = 0,1,2,…,n... Нехай Апроксимуємо і у кожному внутрішньому вузлі (i = 1, 2, …, n-1) центральними різницями , і на кінцях відрізка – односторонніми скінченнорізницевими апроксимаціями , .

Використовуючи ці формули, одержуємо різницеву апроксимацію вихідного крайового завдання: