Контрольная работа: Метод скінчених різниць в обчислювальній математиці

Зміст

Постановка задачі

Вступ

1 Теоретична частина

2 Програмна реалізація

Список використаної літератури

Постановка задачі

Використовуючи метод кінцевих різниць , розв’язати крайову задачу для звичайного диференціального рівняння

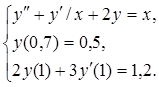
Вступ

Нехай потрібно чисельно розв’язати задачу Коші для звича-йного диференціального рівняння першого порядку, тобто знайти наближений розв’язок диференціального рівняння y=F(x,y), що задовольняє початковій умові y(x)=y.Чисельне розв’язання задачі полягає в побудові таблиці наближених значень y,y,y,...,y-розв’язку рівняння y=(x ) у точках x,x,x,...,x - вузлах сітки .

y

y_n *

y₃ *

y₂ *

y₁ *

y₀ *

O x₀ x₁ x₂ x₃ x_n x

На рисунку * позначені точки, що відповідають наближено-му розв’язку задачі Коші. Треба зазначити, що частіше використо-вують систему рівновіддалених вузлів x =x + ih (i=1,2,..,n) , де h - крок сітки

( h > 0 ) .

1 Теоретич н а част ина

Методи Рунге-Кутта

Різні представники цієї категорії методів потребують більшого чи меншого об’єму обчислень і відповідно забезпечують більшу чи меншу точність. При розв’язанні конкретної задачі виникають питання, якою із формул Рунге-Кутта доцільно скористатися і як вибрати крок сітки.

Якщо неперервна й обмежена разом із своїми четвертими похідними, то гарні результати дає метод четвертого порядку. Він описується системою наступних п'яти співвідношень:

1

2

3 ();

4

5

--> ЧИТАТЬ ПОЛНОСТЬЮ <--