Контрольная работа: Метод структурно-логічного кодування
Для оцінки коректуючих властивостей МІД побудуємо залежність
![]()
при різній довжині n вершин.
При визначенні вірогідності помилки МІД РМІД (5) враховувалися тільки ті варіантипомилокt, які приводили до помилкового прийому, тобто по суті справи до неправильного декодування МІД, що визначається точніше як ймовірність помилки декодування фрагмента кодової комбінації СЛК, тобто ЄКФ.
Аналіз фрагментарного декодування СЛК, на основі залежності ![]() при n=3,4,5 представлений на рис.3.6, показав, що вплив розрядності n вершин куба
при n=3,4,5 представлений на рис.3.6, показав, що вплив розрядності n вершин куба ![]() на ймовірність помилки декодування РМІД практично відсутній. У достатньо важких каналах при
на ймовірність помилки декодування РМІД практично відсутній. У достатньо важких каналах при ![]() фрагментарне декодування СЛК зіставно по ймовірності помилки декодування з згортковим кодом, що виправляє помилки t
фрагментарне декодування СЛК зіставно по ймовірності помилки декодування з згортковим кодом, що виправляє помилки t![]() 2, що указує на можливість успішного використання кодів СЛК в реальних каналах передачі даних.
2, що указує на можливість успішного використання кодів СЛК в реальних каналах передачі даних.
2. Визначення ймовірності помилкового декодування ЄКФ
Використання МІД як єдиного кодуючого формату, тобто кодової комбінації СЛК, як це витікає з аналізу, не є достатньо ефективним, оскільки фрагментарне використання коду СЛК поступається по ймовірності помилки декодування відомим коректуючим кодам, зокрема згортковим кодом, в каналах з ймовірністю помилки ![]() .
.
Нехай в якості ЄКФ прийнята послідовність вершин куба ![]() 3 , тобто n=3. Прийнятий куб
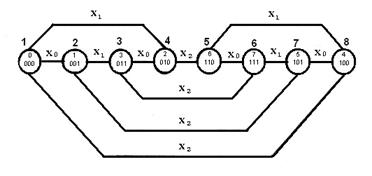
3 , тобто n=3. Прийнятий куб![]() 3 містить два мінімальні інтервали декодування МІД1 і МІД2 , що складаються з 4-х вершин кожен (рис.1).
3 містить два мінімальні інтервали декодування МІД1 і МІД2 , що складаються з 4-х вершин кожен (рис.1).
Нехай всі вершини МІД1 повністю відновлені, що указує на те, що було спотворене не більше однієї вершини в МІД1 . Тоді для повного відновлення всіх вершин в МІД2 необхідне знання відповідної змінної розгортання. Як видно з рис.5 для визначення цієї змінної необхідно і достатньо, щоб тільки одна з 4-х вершин МІД2 була б прийнята коректно, оскільки кожна з вершин МІД1 пов'язана з відповідною вершиною МІД2 по однаковій змінній (на рис. 3.7 такою змінною виступає ![]() ). Тому для будь-якої з вершин МІД2 (5,6,7,8), прийнятої коректно, можливо визначення змінної
). Тому для будь-якої з вершин МІД2 (5,6,7,8), прийнятої коректно, можливо визначення змінної ![]() , що розгортає МІД1 в ЄКФ, тобто куб
, що розгортає МІД1 в ЄКФ, тобто куб ![]() 3 .
3 .
Інші три вершини МІД2 можуть бути прийняті з помилками на етапі визначення змінної розгортання ![]() , оскільки надалі на цьому етапі відновлення всі помилки у вершинах МІД2 виправляються. У межах МІД в якості породжуючих використовуються 2 змінні розгортання (у нашому прикладі це
, оскільки надалі на цьому етапі відновлення всі помилки у вершинах МІД2 виправляються. У межах МІД в якості породжуючих використовуються 2 змінні розгортання (у нашому прикладі це ![]() і
і ![]() ). Одна змінна, що залишилася (
). Одна змінна, що залишилася (![]() у нашому прикладі) використовується для повного відновлення всіх вершин в МІД2 , а отже і всього ЄКФ. Якби в якості ЄКФ виступав куб
у нашому прикладі) використовується для повного відновлення всіх вершин в МІД2 , а отже і всього ЄКФ. Якби в якості ЄКФ виступав куб![]() , то, при повністю відновлених вершинах одного МІД, для правильного прийому всіх вершин
, то, при повністю відновлених вершинах одного МІД, для правильного прийому всіх вершин
ЄКФ необхідне знання відповідних змінних розгортання на кожному етапі
перетворення МІД в ЄКФ кубів![]() .
.
В загальному випадку таких змінних повинно бути n-2, оскільки в МІД використовується 2 змінні розгортання з всієї кількості ![]() . У зв'язку з вищевикладенимсправедлива.
. У зв'язку з вищевикладенимсправедлива.
 |
̲?1 ̲?2
Рис.1
Для повного відновлення всіх вершин ЄКФ куба Еп необхідно і достатньо при коректно прийнятому одному МІД наявність хоча би однієї, прийнятої безпомилково вершини в межах відновлюваного куба ![]() на кожному етапі перетворення.
на кожному етапі перетворення.
Це дійсно так, оскільки наявність однієї правильної вершини в межах відновлюваного куба, окрім відновлених вершин на попередніх етапах, дає можливість визначити змінну відновлення однозначно.
Для n-розрядної вершини ймовірність помилкового прийому з урахуванням одночасності збою ![]() розрядів і правильного прийому n-
розрядів і правильного прийому n-![]() розрядів складе
розрядів складе ![]() . Число варіантів збою
. Число варіантів збою ![]() розрядів очевидно рівно
розрядів очевидно рівно ![]() . Зрозуміло, що кількість збитих розрядів в межах оцінки вершини може змінюватись від 1 до n. У такому разі ймовірність помилкового визначення змінної відновлення із-за неправильного прийому однієї вершини у межах відновлюваного n- мірного куба
. Зрозуміло, що кількість збитих розрядів в межах оцінки вершини може змінюватись від 1 до n. У такому разі ймовірність помилкового визначення змінної відновлення із-за неправильного прийому однієї вершини у межах відновлюваного n- мірного куба ![]() буде рівна
буде рівна
![]() (2)
(2)
Ймовірність Р' визначає, по суті справи, ймовірність помилкового декодування чергового відновлюваного МІД в межах ЄКФ куба ![]() . Тоді ймовірність помилкового декодування ЄКФ куба
. Тоді ймовірність помилкового декодування ЄКФ куба ![]() з урахуванням ймовірності помилки РМ1Д (3.25) буде визначатьсятаким чином.
з урахуванням ймовірності помилки РМ1Д (3.25) буде визначатьсятаким чином.
Ймовірність помилкового декодування ЄКФ визначається ймовірністю помилки МІД РМ1Д і ймовірністю помилки змінної відновлення ![]()
![]() (3)
(3)
де РМ1Д - ймовірність помилки МІД п -мірного куба Е![]() , Р' - ймовірність помилки змінної відновлення .
, Р' - ймовірність помилки змінної відновлення .
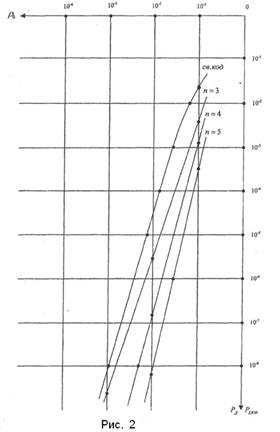
Використовуючи вираз (3) побудуємо залежність ![]() (рис.2) для
(рис.2) для ![]() У тих же координатах розмістимо залежність
У тих же координатах розмістимо залежність ![]() для згорткового коду, що виправляє всі одиночні та двійні помилки. У відміну від фрагментарного декодування СЛК аналіз залежностей
для згорткового коду, що виправляє всі одиночні та двійні помилки. У відміну від фрагментарного декодування СЛК аналіз залежностей ![]() показав, що з ростом
показав, що з ростом ![]() ,тобто із збільшенням мірності куба ЄКФ, кодової комбінації кода СЛК, значно збільшується виграш у завадостійкості, тобто зменшується ймовірність декодування
,тобто із збільшенням мірності куба ЄКФ, кодової комбінації кода СЛК, значно збільшується виграш у завадостійкості, тобто зменшується ймовірність декодування ![]() .
.
Порівнюючи Р![]() для згорткового коду і РЕКФ для n=3,4,5 помічаємо, що для n=3 при
для згорткового коду і РЕКФ для n=3,4,5 помічаємо, що для n=3 при ![]() (ймовірність збою біта в каналі з незалежними помилками) виграш складає в першому наближенні 1 порядок
(ймовірність збою біта в каналі з незалежними помилками) виграш складає в першому наближенні 1 порядок
(Р![]() =2
=2![]() 10
10![]() ,РЄКФ =2
,РЄКФ =2![]() 10
10![]() ). Для n=4 виграш складає 2 порядки (Р
). Для n=4 виграш складає 2 порядки (Р![]() =2
=2![]() 10
10![]() , РЄКФ =1,5
, РЄКФ =1,5![]() 10
10![]() ), а для n=5 - більш, чим 3 порядки (Р
), а для n=5 - більш, чим 3 порядки (Р![]() =2
=2![]() 10
10![]() , РЄКФ =8
, РЄКФ =8![]() 10
10![]() ). У важкому каналі з
). У важкому каналі з ![]() виграш в завадостійкості для СЛК коду складає від 0,5 порядку (n=3) до 1,5 порядку (n=5). Крім того, із зменшенням вірогідності помилки в каналі
виграш в завадостійкості для СЛК коду складає від 0,5 порядку (n=3) до 1,5 порядку (n=5). Крім того, із зменшенням вірогідності помилки в каналі ![]() до
до ![]() виграш в завадостійкості для коду СЛК, принаймні, не зменшується, особливо для n=4,5 , тобто як нахил прямих декодування до осі абсцис в порівнянні з згортковим кодом зменшується. Таким чином, використання структурно-логічних кодів в каналах з незалежними помилками забезпечує істотні переваги взавадостійкості, особливо у важких каналах з
виграш в завадостійкості для коду СЛК, принаймні, не зменшується, особливо для n=4,5 , тобто як нахил прямих декодування до осі абсцис в порівнянні з згортковим кодом зменшується. Таким чином, використання структурно-логічних кодів в каналах з незалежними помилками забезпечує істотні переваги взавадостійкості, особливо у важких каналах з ![]() і каналах середньої тяжкості з
і каналах середньої тяжкості з![]() .
.
Висновок
Проведений аналіз основних особливостей коректуючих властивостей структурно-логічних кодів інфімумних диз'юнктивних нормальних форм БФ для каналів з незалежними помилками.
Визначена ймовірність помилкового декодування ЄКФ коду СЛК