Контрольная работа: Методологія обробки статистичних даних
1. Потрібно встановити залежність y![]() = f (x
= f (x![]() ), де y
), де y![]() - обсяг перевезень руди від кар'єра до збагачувальної фабрики, а x
- обсяг перевезень руди від кар'єра до збагачувальної фабрики, а x![]() - відстань транспортування, що дозволить визначити норму виробітку водія автомобіля для різної відстані перевезень. Вимірюється обсяг перевезень y
- відстань транспортування, що дозволить визначити норму виробітку водія автомобіля для різної відстані перевезень. Вимірюється обсяг перевезень y![]() при різних відстанях (внутрішня регульована змінна x
при різних відстанях (внутрішня регульована змінна x![]() = 2,2; 2,8; 3,3; 4,0; 4,9; 5,4; 6,0 і 7,5 км), де як незалежні зовнішні змінні прийняті день тижня (ПН,ВТ,СР,ЧТ), водій (А,B,C,D) та автомобіль (Z,Y,X,W).
= 2,2; 2,8; 3,3; 4,0; 4,9; 5,4; 6,0 і 7,5 км), де як незалежні зовнішні змінні прийняті день тижня (ПН,ВТ,СР,ЧТ), водій (А,B,C,D) та автомобіль (Z,Y,X,W).
2. Кожна регульована змінна поєднується у рандомізованому плані з іншими незалежними факторами так, щоб в сукупності їх значень не було повторювань будь-якого фактору як по горизонталі, так і по вертикалі ( табл. 3.1). Таким чином кожний водій кожного дня працює на різній відстані перевезень та на іншому автомобілі і кожного дня ці умови не повторюються для інших водіїв.
Таблиця 3.1
Рандомізований план проведення спостережень за обсягами перевезень руди
| Блок 1 | ||||
| Водії | День тижня | |||
| ПН | ВТ | СР | ЧТ | |
| A | 2,2W | 2,8Y | 4W | 3,4Z |
| B | 3,4W | 4Z | 2,8X | 2,2Y |
| C | 4Y | 2,2X | 3,4X | 2,8W |
| D | 2,8Z | 3,4Z | 2,2Y | 4X |
| Блок 2 | ||||
| Водії | День тижня | |||
| ПН | ВТ | СР | ЧТ | |
| A | 4,9X | 5,4Y | 6W | 7,5X |
| B | 7,5Y | 4,9Z | 5,4X | 6Y |
| C | 6Z | 7,5W | 4,9Y | 5,4Z |
| D | 5,4W | 6X | 7,5Z | 4,9W |
Усереднення отриманих значень такого плану за регульованим фактором (відстань перевезення) дозволяє провести повну рандомізацію експерименту за всіма нерегульованими змінними (день тижня, водій, автомобіль), тим самим мінімізується випадковий вплив останніх на досліджувану ознаку.
3. Відтак, провівши спостереження, згідно зі складеним планом для кожної відстані перевезень отримаємо чотири значення обсягу перевезень (табл. 3.2), на підставі яких , відповідно, виводиться їх середнє значення.
Таблиця 3.2
Обсяги перевезень руди
Відстань перевезення x | Обсяг перевезення y | Норма виробітку yзм, т/зміну | |||
| 2,2 | 26 | 27,5 | 26 | 24,5 | 26,00 |
| 2,8 | 23,7 | 25,3 | 22,3 | 22,3 | 23,40 |
| 3,4 | 21,6 | 22,8 | 21,2 | 20,8 | 21,60 |
| 4 | 19,8 | 20,6 | 20,1 | 19,4 | 20,00 |
| 4,9 | 18,1 | 19,9 | 19 | 18 | 18,75 |
| 5,4 | 16,6 | 18,1 | 18,1 | 16,8 | 17,40 |
| 6 | 15,2 | 16,4 | 17,2 | 15,7 | 16,00 |
| 7,5 | 14 | 14,9 | 16,3 | 14,7 | 15,00 |
4. Отримані норми виробітки є результатом збалансування умов експерименту і можуть бути використані для управління випадковими параметрами процесу транспортування через їх відповідність закономірності розподілу випадкових величин.
Завдання № 4
Регресійна модель. Коефіцієнти детермінації і кореляції
З використанням середньостатистичних даних, отриманих у результаті виконання завдання 3, встановіть кореляційну залежність будь-якого техніко-економічного показника діяльності організації (підприємства, виробничого підрозділу, механізму тощо) від однієї з керованих факторних перемінних (ознак), які впливають на цей показник. З цією метою виконайте наступне:
1) побудуйте графічну залежність;
2) виберіть форму рівняння зв’язку для описання вказаної залежності;
3) встановить коефіцієнти рівняння кореляції та напишіть це рівняння;
4) оцініть тісноту зв’язку між ознаками, що корелюють, для чого розрахуйте коефіцієнт кореляції, його похибку та надійність;
5) сформулюйте висновок стосовно можливості використання одержаного рівняння кореляції для прогнозування показника, який розглядається у цьому завданні.
Виконання завдання
У результаті проведення дослідження були отримані результати спостережень за обсягом перевезень руди автомобілями на різну відстань (табл.4.1). Необхідно встановити залежність між обсягом виробітку автомобіля (y) та відстанню перевезень (x) і перевірити отриману залежність показників на адекватність.
1. Будується графічна залежність за результатами спостережень у вигляді графіку функції y = f (x), що проходить через точки перетину всіх наявних даних досліджуваних ознак (рис. 4.1).
Таблиця 4.1
Обсяги перевезень на різну відстань
| Відстань перевезення, x, км | Норма виробітку yзм, т/зміну |
| 2,2 | 26 |
| 2,8 | 23,4 |
| 3,4 | 21,6 |
| 4 | 20 |
| 4,9 | 18,75 |
| 5,4 | 17,4 |
| 6 | 16 |
| 7,5 | 15 |
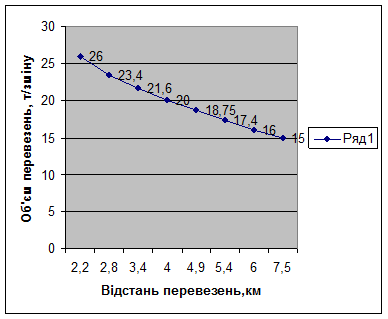
Рис. 4.1. Залежність обсягу виробітку від відстані перевезення
2. Виходячи з рис. 4.1 є очевидним, що між показниками існує лінійна залежність типу y = а + bx: поступове збільшення відстані перевезення обумовлює відповідне зменшення обсягу виробітку.
3. Визначаються коефіцієнти регресії а та b за формулами (4.1) і (4.2). Отримано: b = - 1,5, a = 26,6. Отже, рівняння регресії має наступний вигляд: y = -1,5x + 26,6.
4. Розраховується коефіцієнт кореляції ознак, що досліджуються, за формулою (4.3). Для встановленого рівняння регресії r = 0,98, що свідчить про дуже тісний зв’язок між факторним та результативним показниками.
Встановлюється погрішність коефіцієнту кореляції та його надійність за виразами відповідно (4.4) та (4.5). Ці характеристики дорівнюють: S![]() = 0,08, М = 12,25.
= 0,08, М = 12,25.
5. Отриманий коефіцієнт кореляції, а також його погрішність та надійність свідчать про стійкий зв’язок між корельованими ознаками, що робить модель парної кореляції придатною для використання у практичних розрахунках норми виробітку.
Завдання № 5