В соответствии с проведенными вычислениями уравнения наблюдателя принимают вид:

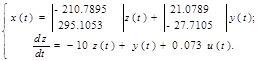
2. Оценивание вектора состояний с помощью наблюдателя Люенбергера

Зададим полученные коэффициенты в MatLab.

a1= -10;

a2=1;

b1= - 0. 0730 ;

;

В среде Simulinkсистемы Matlabпостроим структурную схему объекта и наблюдателя.

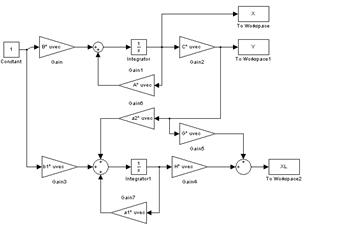
Рис 1 – Simulink -модель объекта и наблюдателя.

На данной модели приняты обозначения:

X,Y– вектор состояния и вектор изменения объекта;

XL– вектор состояния наблюдателя (т.е. оценка вектора состояния объекта).

Запись A*uvec, B*uvec, C*uvec, G*uvec, H*uvec, a1*uvec, a2*uvecи b1*uvecобозначает векторное умножение A, B, C, Gили Hи скалярных величин a1, a2, b1 на соответствующий входной сигнал.

Построим графики вектора состояния

t =0:0.1:10;

figure(1);

plot(t, X(:,1),'b',t,XL(:,1),'or');

grid;

figure(2);

plot(t, X(:,2),'b',t,XL(:,2),'or');

grid;

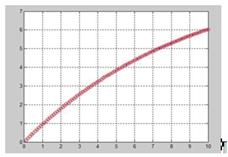
Рис. 2 – истинные и восстановленные значения координат первой компоненты вектора состояния системы

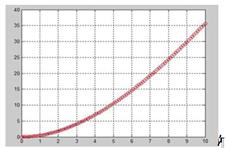
Рис. 3 – истинные и восстановленные значения координат второй компоненты вектора состояния системы

На рисунках 2 и 3 линией показаны истинные кривые значения вектора координат объекта, а символами ‘o’ – восстановленные. Из графиков можно сделать вывод, что при отсутствии помех, в «идеальных условиях», с помощью наблюдателя пониженного порядка можно очень точно оценить координаты вектора состояния. Но в зашумленных условиях, наблюдатель Люинбергера ведет себя неадекватно, т.к., в отличие от наблюдателя полного порядка (фильтр Калмана), оцениваются и учитываются лишь неизвестные компоненты вектора состояния. Если же на выход системы подать помеху, то в системе при измерении, наблюдатель неверно оценивает координаты вектора состояния.

Заключение