Контрольная работа: Нелинейное уравнение и интервал изоляции корня

Вывод

Произведем вычисления согласно представленному выше алгоритму. Необходимо определить корень методом касательных с погрешностью.

Все условия для выполнения данного метода(указаны в теоретической части) выполняются.

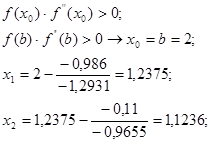
Нашли корень за 2 шага. Проведем вычисления в системе MathCAD.

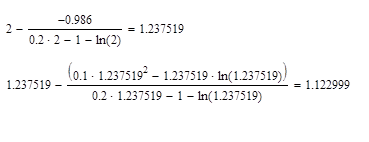
В системе MathCAD мы нашли корень так же за 2 шага.

VI. Уточнение корня методом простой итерации.

Отделение корней, нахождение отрезка изоляции

[c;d]=[a-h;b+h]

Приведение уравнения

f(x)=0 к виду x=g(x)

n=0

n=n+1

Вывод

Произведем вычисления согласно представленному выше алгоритму. Необходимо определить корень методом простой итерации с погрешностью.

Все условия для выполнения данного метода(указаны в теоретической части) выполняются.

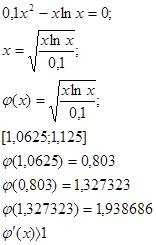
Значит, итерационный процесс не применим, расходится и не позволяет получить решение.

Вывод: Изучили различные методы уточнения корней нелинейных уравнений (метод половинного деления, хорд, касательных, простой итерации). На основе полученных нами результатов можно сделать вывод о том, что высокую скорость сходимости при решении уравнений дает метод хорд и метод касательных. Скорость сходимости методов половинного деления и простой итерации небольшие, но они наиболее легко реализуются на ЭВМ.