Контрольная работа: О некоторых свойствах линейных циклических кодов. Проблемы передачи информации

Выполнила студентка

Суханова С. А.

Гр. УК-04з, МТФ

Проверил преподаватель

Кузнецов И. И.

2007 г.

Содержание

1. Циклические коды. Основные понятия и определения. Построить порождающую матрицу циклического кода с g(х) = 1+х+х*3

1.1 Циклические коды

1.2 Основные параметры циклических кодов

1.3 Основные понятия и определения

1.4 Построить порождающую матрицу циклического кода с g(х) = 1+х+х*3

2. Понятие открытой системы

2.1 Модель OSI

2.2 Понятие «открытой системы»

Список литературы

1. Циклические коды. Основные понятия и определения. Построить порождающую матрицу циклического кода с g (х) = 1+х+х*3

1.1 Циклические коды

Циклические коды - это целое семейство помехоустойчивых кодов, включающее в себя в качестве одной из разновидностей кодов Хэмминга, но в целом обеспечивающее большую гибкость с точки зрения возможности реализации кодов с необходимой способностью обнаружения и исправления ошибок, определяемой параметром d0, по сравнению с кодами Хэмминга (для которых d0=3 или d0=4). Одним из классов циклических кодов, способность исправлять многократные ошибки, являются коды БЧХ. Широкое использование циклических кодов на практике обусловлено также простотой реализации соответствующих кодеров и декодеров. Основные свойства и само название циклических кодов связаны с тем, что все разрешенные комбинации бит в передаваемом сообщении (кодовые слова) могут быть получены путем операции циклического сдвига некоторого исходного кодового слова:

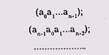
Циклические коды задаются с помощью так называемых порождающих полиномов (многочленов) g(x) степени r = n-k, являющийся сомножителем двучлена xⁿ +1, и их корней. Кроме того, вводятся понятия полинома исходного сообщения. Для этих полиномов, представляющих собой, по существу, альтернативную запись чисел в двоичной системе счисления, определяются операции сложения, умножения и деления, необходимые для организации кодирования и декодирования сообщения. Все эти операции выполняются по модулю 2.

Кодовые слова представляются в виде многочленов:

1.2 Основные параметры циклических кодов

Длина кода - n; Длина информационной последовательности - k; Длина проверочной последовательности - r=n-k; Кодовое расстояние кода - d₀ ; Скорость кода - R=k/n; Избыточность кода - R; Вероятность обнаружения ошибки (искажения) - Р_ОО ; Вероятность не обнаружения ошибки (искажения) - Р_НО .- коэффициенты из поля GF(q).

1.3 Основные понятия и определения

Кодовое расстояние между двумя кодовыми словами (расстояние Хэмминга) - это число позиций, в которых они отличаются друг от друга. Кодовое расстояние кода - это наименьшее расстояние Хэмминга между различными парами кодовых слов. Основные зависимости между кратностью обнаруживаемых ошибок t₀ , исправляемых ошибок t_u , исправлением стираний t_c и кодовым расстоянием d₀ кода:

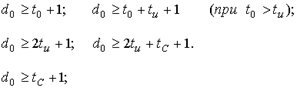
Стиранием называется "потеря" значения передаваемого символа в некоторой позиции кодового слова, которая известна. Код, в котором каждое кодовое слово начинается с информационных символов и заканчивается проверочными символами, называется систематическим. Если код построен над полем GF(2), то коэффициенты принимают значения 0 или 1 и код называется двоичным. Длина циклического кода называется примитивной и сам код называется примитивным, если его длина n=q^m -1 над GF(q). Если длина кода меньше длины примитивного кода, то код называется укороченным или непримитивным. Общее свойство кодовых слов циклического кода - это их делимость без остатка на некоторый многочлен g(x), называемый порождающим. Результатом деления двучлена xⁿ +1 на многочлен g(x) является проверочный многочлен h(x). При декодировании циклических кодов используются многочлен ошибок e(x) и синдромный многочлен S(x). Многочлен ошибок степени не более (n-1) определяется из выражения

--> ЧИТАТЬ ПОЛНОСТЬЮ <--