Контрольная работа: О некоторых свойствах линейных циклических кодов. Проблемы передачи информации

где - многочлены, отображающие соответственно принятое (с ошибкой) и переданное кодовые слова. Ненулевые коэффициенты в е(x) занимают позиции, которые соответствуют ошибкам. Синдромный многочлен, используемый при декодировании циклического кода, определяется как остаток от деления принятого кодового слова на порождающий многочлен, т.е.

или

Следовательно, синдромный многочлен зависит непосредственно от многочлена ошибок е(х). Это положение используется при построении таблицы синдромов, применяемой в процессе декодирования. Эта таблица содержит список многочленов ошибок и список соответствующих синдромов, определяемых из выражения (см. таблицу 4).

Таблица 4
(x)	S(x)
1	Rg(x) [1]
X	Rg(x) [x]
X2	Rg(x) [x2]
	
	
	
X+1	Rg(x) [x+1]
X2 +1	Rg(x) [x2+1]
	
	
	

В процессе декодирования по принятому кодовому слову вычисляется синдром, затем в таблице находится соответствующий многочлен е(х), суммирование которого с принятым кодовым словом дает исправленное кодовое слово, т.е.

Перечисленные многочлены можно складывать, умножать и делить, используя известные правила алгебры, но с приведением результата по модулю 2, а затем по модулю xⁿ +1, если степень результата превышает степень (n-1). Примеры.

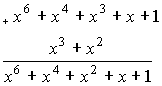
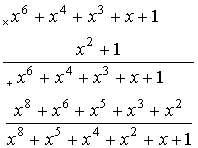
Допустим, что длина кода n=7, то результат приводим по модулю x⁷ +1.

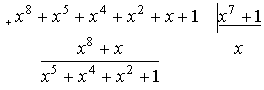
При построении и декодировании циклических кодов в результате деления многочленов обычно необходимо иметь не частное, а остаток от деления. Поэтому рекомендуется более простой способ деления, используя не многочлены, а только его коэффициенты (вариант 2 в примере).

Пример.

1. 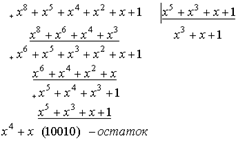2.

Циклический код может быть задан порождающей g(x) и проверочной h(x) матрицами. Для построения достаточно знать порождающий и проверочный многочлены. Для не систематического циклического кода матрицы строятся циклическим сдвигом порождающего и проверочного многочленов, т. е. путем их умножения на х.

Одна из основных задач, стоящих перед разработчиками устройств защиты от ошибок при передачи дискретных сообщений по каналам связи является выбор порождающего многочлена для построения циклического кода, обеспечивающего требуемое минимальное кодовое расстояние для гарантийного обнаружения и исправления t–кратных ошибок.

Существуют специальные таблицы по выбору порождающего многочлена в зависимости от предъявляемых требований к корректирующим возможностям кода. Однако у каждого циклического кода имеются свои особенности формирования порождающего многочлена. Поэтому при изучении конкретных циклических кодов будут рассматриваться соответствующие способы построения порождающего многочлена.

1.4. Построить порождающую матрицу циклического кода с g (х) = 1+х+х*3

Для циклического (7,4)-кода с порождающим многочленом g(x)=1+х+х*3 матрицы G_(n,k) имеет вид:

1+х+х*3 1+х+х*3 1 1 0 1 0 0 0

(1+х+х*3)х х+х*2+х*4 0 1 1 0 1 0 0

G(7,4) = (1+х+х*3)х*2 = х*2+х*3+х*5 = 0 0 1 1 0 1 0

(1+х+х*3)х*3 х*3 +х*4+х*6 0 0 0 1 1 0 1

2. Понятие открытой системы

2.1 Модель OSI

При реализации сетей стремятся использовать стандартные протоколы (формализованные правила, определяющие последовательность и формат сообщений, которыми обмениваются сетевые компоненты, лежащие на одном уровне, но в разных узлах). Это могут быть фирменные, национальные или международные стандарты.

В начале 80-х годов ряд международных организаций по стандартизации – ISO (международная организация по стандартизации (InternationalOrganizationforStandardization, часто называемое также InternationalStandardsOrganization) представляет собой ассоциацию ведущих национальных организаций по стандартизации разных стран; главным достижением ISO явилась модель взаимодействия открытых систем OSI, которая в настоящее время является концептуальной основой стандартизации в области вычислительных сетей; в соответствии с моделью OSI этой организацией был разработан стандартный стек коммуникационных протоколов OSI), ITU-T(TelecommunicationStandardizationSector) – сектор телекоммуникационной стандартизации; основу деятельности ITU-T составляет разработка международных стандартов в области телефонии, телематических служб (электронной почты, факсимильной связи, телетекста, телекса и т. д.), передачи данных, аудио и видеосигналов.