= 0,4995, Þ = 3,29

М-3,29 = 19,9621 мм

М+3,29 = 20,2476 мм

Для партии деталей проведены измерения координат X,Y двух отверстий 1 и 2. Определить средний размер и среднее квадратическое отклонение размера межцентрового расстояния.

Номер измерения	Значения параметра
X1	X2	Y1	Y2
1	26,792	28,394	29,9	31,911
2	26,787	28,487	29,901	31,922
3	26,79	28,39	29,913	31,914
4	26,792	28,592	29,902	31,899
5	26,791	28,494	29,903	31,898
6	26,782	28,485	29,912	31,91
7	26,792	28,591	29,901	31,891
8	26,792	28,791	29,903	31,902
9	26,787	28,584	29,912	31,898
10	26,793	28,572	29,906	31,907
11	26,79	28,493	29,9	31,899
12	26,794	28,493	29,912	31,898
13	26,786	28,576	29,903	31,889

Для определения среднего размера и среднего квадратического отклонения S воспользуемся следующими формулами:

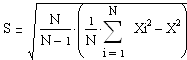
где N=13

= 26,7898 мм = 0,003411895 мм

= 28,534 мм = 0,10339165 мм

= 29,9052 мм = 0,005117842 мм

= 31,9029 мм = 0,009393806 мм

Определим средний размер межцентрового расстояния:

= 2,1318 мм

Определим среднее квадратическое отклонение размера межцентрового расстояния по формуле:

,

где – частная производная по от и – частная производная по от :

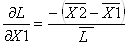= -0,3491

= 0,3491

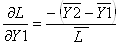= -0,9371

= 0,9371

Т. о. S_L = 0,0375 мм.