Контрольная работа: Оптимальный план загрузки оборудования и транспортных связей

У₁ = =173,84

У₂ = 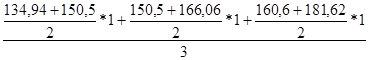=157,37

У₃ =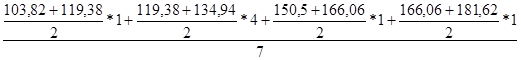₌ 127,48

У₄ = 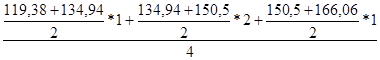=238,09

У₅ = 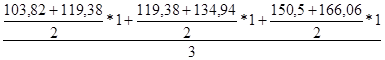=259,5

У₆ = 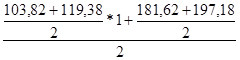=150,5

=

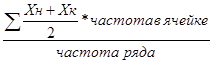
Х₁ = 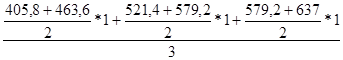=531,03

Х₂ = 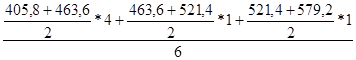=463,6

Х₃ = 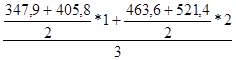=444,3

Х₄ = 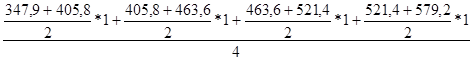=463,59

Х₅ = 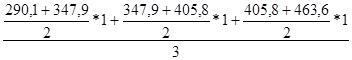=376,85

Х₆ = =608,1

Найдем уравнение регрессии

Y=a_o +a₁ x

a_o и a₁ найдем из системы:

na_o +a_{1 =}

a_o + a₁ =

Построим расчетную таблицу:

№	Х	У	X^2	Y^2	X*Y
1	319	168,1	101761	28257,61	53623,9	151,97
2	358	176,2	128164	31046,44	63079,6	149,63
3	399	159,4	159201	25408,36	63600,6	147,17
4	401	138,9	160801	19293,21	55698,9	147,05
5	419	169,7	175561	28798,09	71104,3	145,97
6	420	123,5	176400	15252,25	51870	145,91
7	425	153,4	180625	23531,56	65195	145,61
8	429	113,4	184041	12859,56	48648,6	145,37
9	455	121,5	207025	14762,25	55282,5	143,87
10	459	134,6	210681	18117,16	61781,4	143,57
11	463	124,5	214369	15500,25	57643,5	143,33
12	465	145,9	216225	21286,81	67843,5	143,21
13	481	154,9	231361	23994,01	74506,9	142,25
14	491	148,7	241081	22111,69	73011,7	141,05
15	517	126,6	267289	16027,56	65452,2	140,09
16	529	128,6	279841	16537,96	68029,4	139,97
17	534	116,2	285156	13502,44	62050,8	139,07
18	561	158,4	314721	25090,56	88862,4	137,05
19	602	111,6	362404	12454,56	67183,2	134,99
20	614	189,4	376996	35872,36	116291,6	134,27
Итого:	9341	2863,5	4473703	419704,69	1330760	2861,74

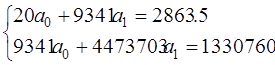
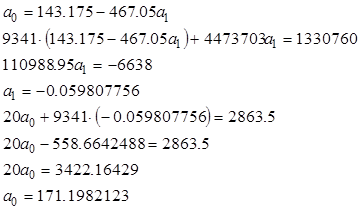
Таким образом, уравнение регрессии получается:

Используя уравнение регрессии, дополним последний столбец расчетной таблицей. Измерим частоту связи в парной корреляции с помощью коэффициента корреляции:

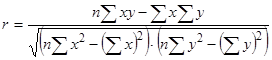
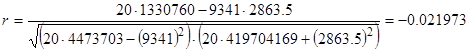
Вывод: коэффициент корреляции r равен - 0,02, что говорит о наличии прямой слабой связи между затратами на единицу продукции и балансовой прибыли предприятия.

Рассчитаем t-критерий Стьюдента: