Контрольная работа: Оптимизация организационных решений

Х₁ – искомое количество квартир в кирпичном доме;

Х₂ – искомое количество квартир в панельном доме.

Целевая функция:

L = Х₁ + Х₂ max

Ограничениями будут неравенства, полученные на основании исходных данных:

1. Арматура 0,6Х₁ + 1,3 Х₂ ≤ 900 ;

2. Пиломатериалы 0,8Х₁ + 0,3 Х₂ ≤ 520 ;

3. Цемент 5Х₁ + 9Х₂ ≤ 7 000 ;

4. Керамическая плитка 0,5Х₁ ≤ 400 ;

5. Трудозатраты 70Х₁ + 50Х₂ ≤ 55 000 ;

6. Х₁ ≥ 0 ;

7. Х₂ ≥ 0 .

Поскольку имеется только два неизвестных, то применим геометрическое решение. Для удобства построений преобразуем не равенства.

1. 6Х₁ + 13 Х₂ ≤ 9 000 ;

2. 8Х₁ + 3 Х₂ ≤ 5 200 ;

3. 5Х₁ + 9Х₂ ≤ 7 000 ;

4. 5Х₁ ≤ 4 000 ;

5. 7Х₁ + 5Х₂ ≤ 5 500 ;

6. Х₁ ≥ 0 ;

7. Х₂ ≥ 0 .

Геометрически ограничения неравенств выражаются в виде открытых полуплоскостей, ограниченных осями координат и линиями, описываемыми равенствами, полученными из выражений ограничений:

1. 6Х₁ + 13 Х₂ = 9 000 ;

2. 8Х₁ + 3 Х₂ = 5 200 ;

3. 5Х₁ + 9Х₂ = 7 000 ;

4. 5Х₁ = 4 000 ;

5. 7Х₁ + 5Х₂ = 5 500 .

Нанесем эти линии на график.

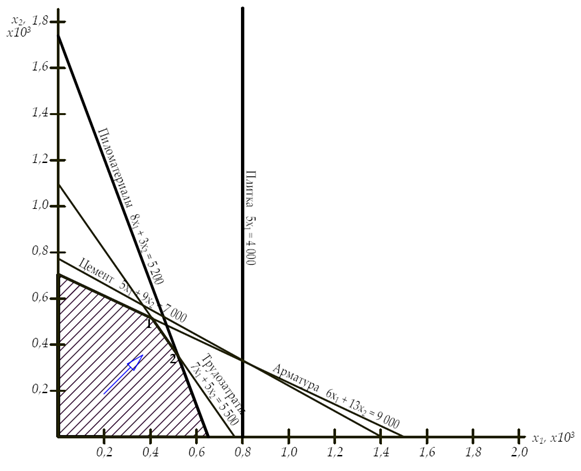
В целом условиям неравенств удовлетворяет заштрихованная область. Оптимальное решение находится на контуре этой фигуры в одной из узловых точек и определяется совместным рассмотрением выражений: