Контрольная работа: Основи теорії сигналів

Спектральний метод аналізу, заснований на поданні сигналу у вигляді суми (або інтегралу) гармонічних складових (гармонік) і подальшому розрахунку проходження кожної з гармонік через коло. Вихідний сигнал знаходиться на основі принципу накладання у вигляді суми відгуків на кожну з гармонік вхідного сигналу. Сукупність гармонік, на які розкладаються сигнали, називається їх спектрами.

Вивчення спектрів розпочинається з періодичних імпульсних відеосигналів.

Імпульсними називаються струми і напруги кінцевої енергії, миттєві значення яких відмінні від нуля впродовж деякого (як правило, досить невеликого) інтервалу часу.

Періодичні послідовності імпульсів (рис. 1) відносяться до періодичних несинусоїдних процесів і знаходять широке використання в радіоелектроніці.

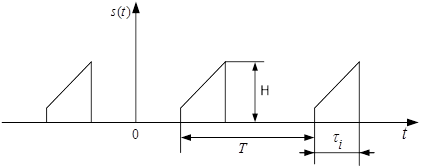
Рисунок 1 – Періодична послідовність імпульсів

Періодичні послідовності імпульсів характеризуються їх формою, тривалістю , періодом повторення (або частотою ), висотою (максимальним значенням) –.

Тривалість імпульсів знаходять на деякому рівні від висоти (у границі на нульовому рівні), або як інтервал часу, в якому міститься визначена потужність імпульсу (зазвичай 90або більше).

Інколи вводиться також вторинний параметр – щілинність:

.

Періодична послідовність імпульсів, описується функцією, яка задовольняє умови Діріхле і може бути подана нескінченим рядом (рядом Фур’є) гармонік з частотами, кратними частотам слідування , :

, (1)

де 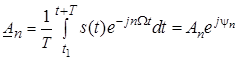– комплексна амплітуда -ї гармоніки,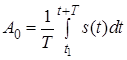 – постійна складова імпульсів (середнє значення).

Сукупність амплітуд гармонік називають спектром амплітуд або амплітудно-частотним спектром (АЧС).

Сукупність початкових фаз називають спектром фаз або фазочастотним спектром (ФЧС).

АЧС і ФЧС зображують у вигляді графіків, в яких за віссю абсцис відкладають частоту ( або ), а за віссю ординат – амплітуди гармонік у АЧС і початкові фази у ФЧС (рис. 2). Властивістю спектра періодичного коливання є поступове зменшення амплітуд гармонік зі зростанням їх частоти. Це дозволяє оперувати з нескінченними межами сум у (1), а з сумами обмеженими . 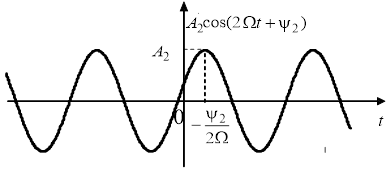Кожній парі ординат графіків АЧС і ФЧС відповідна частота однієї з гармонік, тобто ,, повністю визначають параметри цієї гармоніки. Наприклад, на рис. 3 побудована у функції часу друга гармоніка спектра з частотою , амплітудою і зсувом максимуму косинусоїди вправо (відносно ) на відрізок часу пропорційний .

Оскільки середня потужність періодичного сигналу є сумою потужностей гармонічних складових сигналу і потужності сталої складової, ширина спектра визначається частотою коливання з амплітудою , яка ще впливає на значення середньої потужності на заданому рівні:

.

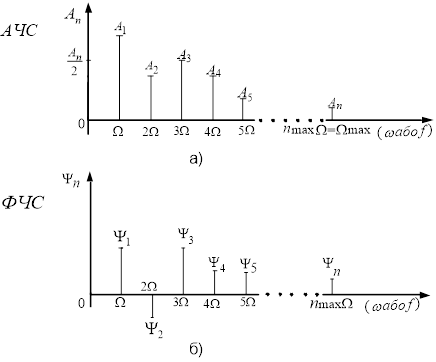
Рисунок 2 – Графіки АЧС (а) і ФЧС (б)

У тих випадках, коли – парна функція часу, в (1) дорівнює нулю або . Для непарної функції, навпаки, ряд Фур’є складається тільки із синусоїдних коливань, тобто дорівнює або .

У двох послідовностях імпульсів і , які відрізняються тільки початком відліку часу, АЧС однакові, а відрізняються тільки їх ФЧС. Дійсно, якщо , тоді

(2)

Таким чином, при зсуві сигналу на фази його гармоніки змінюється на .

Як ілюстрації наведемо результати розкладу в ряд Фур’є періодичної послідовності прямокутних імпульсів (рис. 4), яку аналітично можна записати у вигляді:

Рисунок 4 – Періодична послідовність прямокутних імпульсів

--> ЧИТАТЬ ПОЛНОСТЬЮ <--