Контрольная работа: Основные электроматериалы
Сегнетовая соль - εr =1500…20000
Титанат бария εr =7000…9000
Первоксид - εr =800…10000
Пирониобат кадмия - εr =1000…1500
Приведенная выше классификация диэлектриков отражает в достаточной степени основные электрические свойства.
2. Объяснить, в чем заключается различие между понятиями "тангенс угла диэлектрических потерь" и "коэффициент диэлектрических потерь"
Диэлектрическими потерями называют электрическую мощность, затрачиваемую на нагрев диэлектрика, находящегося в электрическом поле.
Потери в энергии в диэлектриках наблюдаются как при переменном, так и при постоянном напряжении, поскольку в технических материалах обнаруживается сквозной ток утечки, обусловленный электропроводностью. При постоянном напряжении, когда нет периодической поляризации, качество материала характеризуется, как указывалось, значениями удельных объемного и поверхностного сопротивлений, которые определяют значение Rиз (см.рис.1.1).
При воздействии переменного напряжения на диэлектрик в нем кроме сквозной электропроводности могут проявляться другие механизмы превращения электрической энергии в тепловую. Поэтому качество материала недостаточно характеризовать только сопротивлением изоляции.
В инженерной практике чаще всего для характеристики способности диэлектрика рассеивать энергию в электрическом поле используют угол диэлектрических потерь, а также тангенс этого угла.
Углом диэлектрических потерь называют угол, дополняющий до 900 угол сдвига фаз φ между током и напряжением в емкостной цепи.
В случае идеального диэлектрика вектор тока в такой цепи опережает вектор напряжения на угол 900 ; при этом угол равен нулю. Чем больше рассеивается в диэлектрике мощность, тем меньше угол сдвига фаз φ и тем больше угол диэлектрических потерь и его функция tg.
Тангенс угла диэлектрических потерь непосредственно входит в формулу для рассеиваемой в диэлектрике мощности, поэтому практически наиболее часто пользуется этой характеристикой.
Рассмотрим схему, эквивалентную конденсатору с диэлектриком, обладающим потерями. Эта схема должна быть выбрана с таким расчетом, чтобы активная мощность, расходуемая в данной схеме, была равно мощности, рассеиваемой в диэлектрике конденсатора, а ток был бы сдвинут относительно напряжения на тот же угол, что и в рассматриваемом конденсаторе.
Поставленную задачу можно решить, заменив конденсатор с потерями идеальным конденсатором с параллельно включенным активным сопротивлением (параллельная схема) или конденсатором с последовательно включенным сопротивлением (последовательная схема). Такие эквивалентные схемы, конечно, не дают объяснения механизма диэлектрических потерь и введены только условно.
Параллельная и последовательная эквивалентные схемы представлены на рис. 2.1.. Там же даны соответствующие диаграммы токов и напряжений. Обе схемы эквивалентны друг другу, если при равенстве полных сопротивлений Z1 = Z2 = Z равны соответственно их активные и реактивные составляющие. Это условие будет соблюдено, если углы сдвига тока относительно напряжения равны и значения активной мощности одинаковы.

Рис. 2.1. Параллельная (а) и последовательная (б) эквивалентные схемы диэлектрика с потерями и векторные диаграммы для них.
Для параллельной схемы из векторной диаграммы
tg = I а / I с = 1 / (ω C р R ); (2.1.)
Ра = U · I а = U 2 ω Ср tg (2.2.)
для последовательной схемы
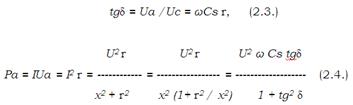
Приравнивая выражения (2.2.) и (2.4.), а также (2.1.) и (2.3.), найдем соотношения между Ср и С s и между R и r:
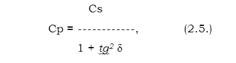
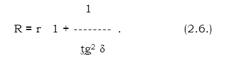
Для доброкачественных диэлектриков можно пренебречь значением tg2 по сравнению с единицей в формуле (2.5.) и считать Ср ≈ С s = С . Выражения для мощности, рассеиваемой в диэлектрике, в этом случае будут также одинаковы у обеих схем:
Ра = U2 ω С tg , (2.7.)
где Ра выражено в Вт; U – в В; ω – в с-1 ; С – в Ф.
Следует отметить, что при переменном напряжении в отличие от постоянного емкость диэлектрика с большими потерями становится условной величиной и зависит от выбора той или иной эквивалентной схемы. Отсюда и диэлектрическая проницаемость материала с большими потерями при переменном напряжении также условна.