.

Найдем определитель ( det) матрицы:

.

; ; .

; ; .

РЕЗУЛЬТАТЫ ОПЫТОВ В ГРАФИЧЕСКОМ ВИДЕ

Построим графики функций Y = a₀ + a₁ X ; Y = a₀ + a₁ X + a₂ X² :

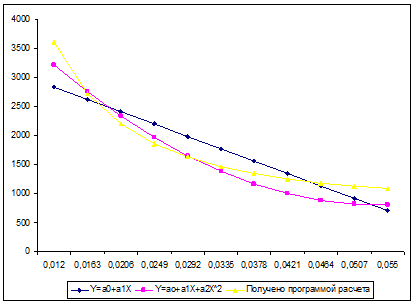
X	0,012	0,0163	0,0206	0,0249	0,0292	0,0335	0,0378	0,0421	0,0464	0,0507	0,055
Y=ao +a1 X	2833,143	2619,9	2406,658	2193,415	1980,172	1766,929	1553,686	1340,443	1127,2	913,9573	700,7144
Y=a0 +a1 X+a2 X2	3215,923	2748,207	2330,714	1963,444	1646,397	1379,574	1162,973	996,5962	880,4424	814,5117	798,8043

ПРОВЕРКА АДЕКВАТНОСТИ И РАБОТОСПОСОБНОСТИ МОДЕЛИ

Для проверки адекватности модели определим абсолютные DY_j и относительные погрешности в каждом из опытов.

DY_j = - Y_j ; ,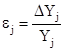

где – расчетное значение функции (отклика) в j-ой точке.

Данные представим в виде таблицы 3.

Табл. 3

j	Y = a0 + a1 X		Y = a0 + a1 X + a2 X2
	DYj		DYj
1	-768,6918	-0,21342	-385,9118	-0,10714
2	-92,531	-0,03411	35,776	0,01319
3	211,2237	0,09621	135,2797	0,06162
4	338,0513	0,1822	108,0803	0,05825
5	353,3076	0,21717	19,5326	0,012
6	305,684	0,20919	-81,671	-0,05589
7	214,109	0,15983	-176,604	-0,13183
8	89,9295	0,07191	-253,9173	-0,20305
9	-46,7877	-0,0398	-293,5453	-0,25004
10	-212,5033	-0,1886	-311,9489	-0,27693
11	-391,8429	-0,35865	-293,753	-0,26887

Просматривая значения этих погрешностей, исследователь может легко понять, какова погрешность предсказания в точках, где проводились опыты, устраивают его или нет подобные ошибки. Таким образом, путем сопоставления фактических значений отклика с предсказанными по уравнению регрессии можно получить достаточно надежное свидетельство о точностных характеристиках модели.

С помощью анализа работоспособности регрессионной модели выясним практическую возможность ее использования для решения какой-либо задачи. Это анализ будем проводить, вычисляя коэффициент детерминации (квадрат корреляционного отношения). Коэффициент детерминации R² вычисляется по формуле:

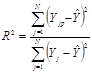
где 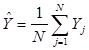– общее среднее значение функции отклика.

.

Вычислим из N опытов необходимые суммы и данные представим в виде таблицы 4.

Табл. 4

Y = a0 + a1 X	Y = a0 + a1 X + a2 X2
j
1	3366863,62479	1136803,18835	1952571,23764
2	893965,95743	727552,24249	853898,13319
3	183613,13271	409247,73017	312848,71152
4	7819,94095	181886,66602	37616,467
5	19619,28834	45470,75597	14328,99238
6	93445,31841	0,00002	147047,20405
7	182633,3815	45474,39816	359786,00774
8	266689,37885	181893,9504	589419,20142
9	351584,44898	409258,65674	602866,06259
10	410205,24101	727568,0054	801506,847
11	454782,94891	1136822,67874	759273,70255
Σ	6231222,66188	5001978,27246	5732724,84892

Для уравнения регрессии Y = a₀ + a₁ X:

Для уравнения регрессии Y = a₀ + a₁ X + a₂ X² :

Т.к. в уравнениях регрессии оба уравнения принято считать работоспособными. В уравнении регрессии вида Y = a₀ + a₁ X + a₂ X²

, а в уравнении регрессии вида Y = a₀ + a₁ X. Из этого следует, что в уравнении вида Y = a₀ + a₁ X + a₂ X² найденное значение регрессии лучше объясняет вариацию в значениях Y (N >> (d+1)), чем в уравнении вида Y = a₀ + a₁ X.

ВЫВОД

В процессе выполнения контрольно-курсовой работы мы научились:

- разрабатывать план проведения вычислительного эксперимента;

- проводить вычислительный эксперимент на ЭВМ и накапливать статистическую информацию;