Контрольная работа: Основы теории вероятности
в). Произведение числа очков делится на N = 8 : кол-во благоприятных исходов m = 5
Вероятность
![]()
Задача № 3
Имеются изделия четырёх сортов, причём число изделий i - го сорта равно ni , i = 1, 2, 3, 4.
Для контроля наудачу берутся m – изделий. Определить вероятность того, что среди них m1 первосортных, m2 , m3 и m4 второго, третьего и четвёртого сорта соответственно.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Задача № 4
В лифт k – этажного дома сели n пассажироа (n<k). Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что: а) все вышли на разных этажах; б) по крайней мере, двое сошли на одном этаже.
k = 11, n = 4
а) Все на разных:
n = 114 = 14641
![]()
![]()
б) Хотя бы два на одном:
![]()
Задача № 5
В двух партиях k1 и k2 % доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них:
а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное.
k1 = 86% , k2 = 32%
A1 - доброкачественные в 1-й партии
A2 - доброкачественные в 2-й партии
а). одно бракованное:
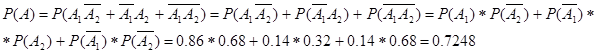
б). два бракованных:
![]()
в). Одно доброкачественное и одно бракованное:
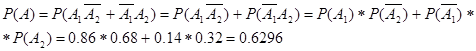
Задача № 6
Из 1000 ламп ni принадлежат i – партии, i = 1, 2, 3. В первой партии 6%, во второй 5%, в третьей 4% бракованных лам. Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа – бракованная.
n1 = 700 n2 = 90 n3 = 210 ![]()
p1 = 0.06 p2 = 0.05 p3 = 0.04
Пусть:
H1 – взяли из 1-й партии
H2 – взяли из 2-й партии
H3 – взяли из 3-й партии
![]()
![]()
![]()
Пусть Bi – брак из i - й партии =>
![]()
![]()
![]()