Контрольная работа: Передаточные функции одноконтурной системы

Отсюда получено:

.

Если обозначить передаточные функции объекта как

и ,

то получается уравнение Y(s) = Wx(s).X(s) + WF(s).F(s). Структурная схема объекта приведена на рис. 3.

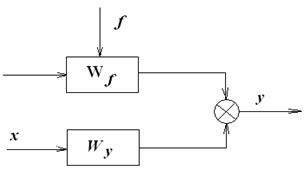
Рис. 3

Характеристическая функция имеет вид:

,

а характеристическое уравнение:

.

Корни этого уравнения равны:

и .

Распределение корней на комплексной плоскости показано на рис. 4:

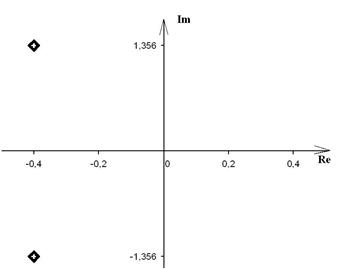
Рис. 4.

Все корни характеристического уравнения лежат в левой полуплоскости, очевидно, что объект устойчив.

2. Дана передаточная функция вида:

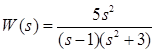
Зная, что по определению, , получим:

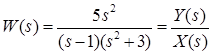, тогда:

.

Раскрывая скобки:

Применяя к полученному выражению обратное преобразование Лапласа, находим искомое дифференциальное уравнение:

.

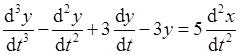Практическая работа № 2

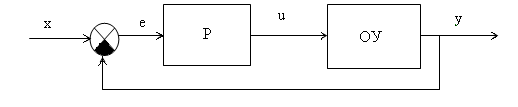
Дана одноконтурная АСР, для которой определена передаточная функция регулятора (Р) с настройками и дифференциальное уравнение объекта управления (ОУ). Требуется определить:

- передаточную функцию разомкнутой системы W∞(s),