Контрольная работа: по Статистике 9
Результаты представить в виде статистической таблицы, сформулировать выводы.
| Количество групп по формуле Стерджесса | Размах вариации | Величина равного интервала | |
| 1+3,22*LOG10(40)=6,16 | 23,2-17=6,20 | 6,2/6,16=1,01 | |
| Средне-годовая стоимость ОС, млн. руб | кол-во предпр-иятий | Расчетные показатели | |||
| общая средне-годовая стоимость ОС | средняя стоимость ОС | общий выпуск кирпича, млн. шт | средний выпуск | ||
| до 18 | 5 | 87,10 | 17,42 | 149,20 | 29,84 |
| 18-19 | 13 | 240,90 | 18,53 | 415,30 | 31,94615 |
| 19-20 | 11 | 215,00 | 19,55 | 393,00 | 35,72727 |
| 20-21 | 0 | 0,00 | 0,00 | ||
| 21-22 | 6 | 129,20 | 21,53 | 217,90 | 36,31667 |
| больше 22 | 5 | 112,40 | 22,48 | 205,50 | 41,1 |
Выводы:
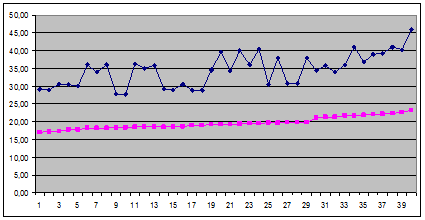
1) Явно прослеживается связь между стоимостью ОС и объемом выпуска: чем больше величина ОС, тем выше объем выпуска.
Это видно, в частности, на графике.
2) Интервал 20-21 пуст, что вообще говоря маловероятно для выборочного метода. Возможна ошибка при сборе статистических сведений.
Это тоже видно на графике: между 29 и 31 ряд резко «подскакивает» вверх.
2. Построить ряд распределения предприятий по физическому объему выпущенной продукции в отчетном году, рассчитав величину интервала по формуле Стерджесса.
Для построенного ряда определить среднюю арифметическую величину, моду, медиану, показатели вариации, показатель асимметрии.
По правилу 3-х сигм проверить соответствие эмпирического распределения нормальному, сформулировать выводы.
| Количество групп по формуле Стерджесса | Размах вариации | Величина равного интервала | |
| 6,16 | 18,10 | 2,94 | |
4
| выпуск кирпича, млн. шт. | кол-во предприятий | Расчетные показатели | ||
| x'i, середина интервала | x'i * fi | кумулята | ||
| 27,8-30,82 | 15 | 29,31 | 439,65 | 15 |
| 30,82-33,84 | 0 | 32,33 | 15 | |
| 33,84-36,86 | 14 | 35,35 | 494,90 | 29 |
| 36,86-39,88 | 5 | 38,37 | 191,85 | 34 |
| 39,88-42,90 | 5 | 41,39 | 206,95 | 39 |
| 42,90-45,92 | 1 | 44,41 | 44,41 | 40 |
| Сумма: | 1377,76 | |||
Средняя арифметическая интервального ВР: 34,44
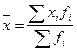
Для надежности, вычисляем среднюю арифметическую несгруппированного ряда:
Сумма: 1380,90
Средняя арифметическая ВР:34,52
Здесь можно заметить небольшие различия, в 0,08 (менее одного процента).
Моду вычисляем по формуле:
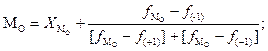
| мода | 29,31 | |
| модальный интервал: | 27,8-30,82 | |
По накопленным частотам, определяем, что медиана находится в 3м интервале
медиана для несгруппированного ряда: Me=(34,6+35)/2
(20 и 21 элемент ранжированной выборки).
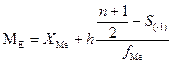=33,84+3,02*((40+1/2)-15)/14 = 39,34
Показатели вариации:
| среднее линейное отклонение | дисперсия (взвешенная) | |||||
| расчетные показатели |  | расчетные показатели | ||||
| x'i- -x | |x'i- -x|fi | x'i- -x | (x'i- -x)2 | (x'i- -x) 2 *f i | ||
| -5,13 | 77,01 | -5,13 | 26,36 | 395,37 | ||
| -2,11 | 0,00 | -2,11 | 4,47 | 0,00 | ||
| 0,91 | 12,68 | 0,91 | 0,82 | 11,49 | ||
| 3,93 | 19,63 | 3,93 | 15,41 | 77,07 | ||
| 6,95 | 34,73 |  | 6,95 | 48,25 | 241,23 | |
| 9,97 | 9,97 | 9,97 | 99,32 | 99,32 | ||
| 154,02 | 824,48 | |||||
| среднее линейное отклонение | 3,85 | дисперсия (взвешенная) | 20,61 | |||
среднее квадратическое отклонение = √ D = √20,61= 4,540
Показатель асимметрии рассчитывается по формуле As = μ3 /σ3 ,
но мы воспользуемся более простой формулой: 
(средняя арифметическая минус мода деленное на среднее квадратическое отклонение).
Показатель асимметрии As = 1,14, что значит, что функция плотности скошена влево: