Величину

називають середнім значенням функції в області .

подвійний інтеграл адитивність

3. Обчислення подвійного інтеграла

Обчислення подвійного інтеграла за формулою (6) як границі інтегральної суми, так само як і у випадку визначеного інтеграла, пов'язане із значними труднощами. Щоб уникнути їх, обчислення подвійного інтеграла зводять до обчислення так званого повторного інтеграла - двох звичайних визначених інтегралів.

Покажемо, як це робиться. Припустимо, що при функція . Тоді, згідно з формулою (7), подвійний інтеграл виражає об'єм циліндричного тіла (рис.3) з основою , обмеженого зверху поверхнею . Обчислимо цей об'єм за допомогою методу паралельних перерізів [6]:

,

де - площа перерізу тіла площиною, перпендикулярною до осі , а та - рівняння площин, які обмежують дане тіло. Перед тим, як обчислювати площу зробимо певні припущення відносно області .

Припустимо спочатку, що область інтегрування обмежена двома неперервними кривими та і двома прямими та , причому для всіх (рис.4). Проведемо через точку , де , пряму, паралельну осі . Ця пряма перетинає криві та в точках і , які називатимемо відповідно точкою входу в область і точкою виходу з області . Ординати цих точок позначимо відповідно та , тоді , .

Рисунок 3 - Циліндричне тіло Рисунок 4 - Область

Визначена таким чином область називається правильною в напрямі осі . Інакше кажучи, область називається правильною в напрямі осі , якщо довільна пряма, яка проходить через внутрішню точку області паралельно осі , перетинає межу області не більше, ніж у двох точках.

Знайдемо тепер площу . Для цього проведемо через точку площину, перпендикулярну осі (рис.3). У перерізі цієї площини і циліндричного тіла утворюється трапеція . Апліката точки лінії при фіксованому є функцією лише , причому змінюється в межах від до . Площа трапеції дорівнює визначеному інтегралу

.

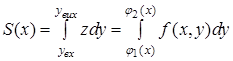Підставивши знайдене значення у формулу і враховуючи формулу (7), отримаємо

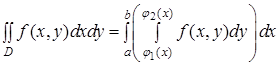
або в зручнішій формі

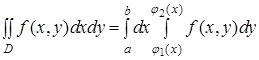. (10)

Це і є шукана формула для обчислення подвійного інтеграла. Праву частину формули (10) називають повторним інтегралом від функції за областю. У повторному інтегралі (10) інтегрування виконується спочатку за змінною (при цьому вважається сталою), а потім за змінною . Інтеграл за змінною називають внутрішнім, а за змінною - зовнішнім. У результаті обчислення внутрішнього інтеграла (в межах від до ) одержуємо певну функцію від однієї змінної . Інтегруючи цю функцію в межах від до , тобто обчислюючи зовнішній інтеграл, отримаємо деяке число - значення подвійного інтеграла. Зауваження Наведені геометричні міркування при одержанні формули (10) можливі у випадку, коли . Проте формула (10) залишається справедливою і в загальному випадку. Зауваження 2. Якщо область обмежена двома неперервними кривими і двома прямими причому для всіх , тобто якщо область правильна в напрямі осі (рис.5), то справедлива формула

. (11)

Тут внутрішнім є інтеграл за змінною . Обчислюючи його в межах від до (при цьому вважається сталою), отримаємо деяку функцію від однієї змінної . Інтегруючи потім цю функцію в межах від до , отримаємо значення подвійного інтеграла.

Зауваження 3. Якщо область правильна в обох напрямах, то подвійний інтеграл можна обчислювати як за формулою (10), так і за формулою (11). Результати матимемо однакові.

Зауваження 4. Якщо область не є правильною ні в напрямі осі ,ні в напрямі осі (тобто існують вертикальні і горизонтальні прямі, які, проходячи через внутрішні точки області, перетинають її межу більше, ніж у двох точках), то таку область необхідно розбити на частини, кожна з яких є правильною областю у напрямі чи . Обчислюючи подвійні інтеграли по правильних областях і додаючи результати (властивість адитивності), знаходимо шуканий подвійний інтеграл за областю . Для випадку, зображеного на рис.6 (область обмежена еліпсами 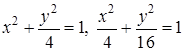і прямою ), при інтегруванні в напрямі осі маємо

.

У напрямі осі тут потрібно було б обчислити повторні інтеграли по семи областях.

Зауваження 5. Повторні інтеграли в правих частинах формули (10) і (11) називаються інтегралами з різним порядком інтегрування. Щобзмінити порядок інтегрування, потрібно від формули (10) перейти до формули (11) або навпаки.

У кожному конкретному випадку, залежно від виду області та підінтегральної функції , потрібно обирати той порядок інтегрування, який призводить до простіших обчислень.

Зауваження 6. Правильну в напрямі осі область коротко позначатимемо так:

.