Контрольная работа: Погрешности вычислений на ЭВМ

Из этой формулы видно, что величина может быть вычислена только при известном значении точного числа А. Если точное значение числа не известно, то используется понятие предельной относительной погрешности

.

В практике вычислений величина определяется по формуле

.

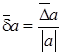Полагают, что эта формула применима, если , В частности, считается нормальным, если или, что то же самое, . В грубых расчетах допускается . Иногда требуется, чтобы .

3. Правила записи приближенных чисел

Для решения инженерных задач часто приходится определять различные числа, как точные, так и приближенные. При этом требуется, чтобы погрешность, возникающая при округлении была бы минимальной.

Пусть некоторое десятичное число представлено его разложением

,

где 10^S – единица разряда S, a_S – цифра разряда, S – номер разряда.

Все цифры числа от первой слева, неравной нулю, до последней цифры справа называются значащими цифрами.

Например, пусть заданы следующие числа:

a₁ = 2.67; a₂ = 0.267; a₃ = 0.00267; a₄ = 0.26700

Тогда для a₁ , a₂ , a₃ имеем 3 значащие цифры и для a₄ - 5 значащих цифр.

Если крайние справа нули не считают значащими, то число записывают в экспоненциальной форме:

,

где m - экспонента, p – порядок числа.

Значащая цифра числа a_S называется верной, если абсолютная погрешность этого числа не превосходит половины единицы разряда S, т. е.

.

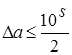Если абсолютная погрешность числа не указана, то все его значащие цифры считают верными.

Под округлением числа а будем понимать его замену числом а’, которое имеет меньшее количество значащих цифр, чем исходное число а. Округление должно производиться таким образом, чтобы возникающая ошибка была минимальной.

Для оценки величины ошибки вводят следующие характеристики:

- абсолютная погрешность округления ;

- относительная погрешность округления .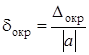

При необходимости могут использоваться их предельные значения:

; .

Если округляется приближенное число, то погрешность полученного числа включает две составляющие:

- погрешность округления;

- погрешность исходного числа.