Контрольная работа: Погрешности вычислений на ЭВМ
1. Если первая из отбрасываемых цифр меньше 5, то последняя сохраняемая цифра не изменяется.
2. Если первая из отбрасываемых цифр больше 5, то последняя сохраняемая цифра увеличивается на 1.
3. Если первая из отбрасываемых цифр равна 5, и за ней идут не нули, то последняя сохраняемая цифра увеличивается на 1.
4. Если первая из отбрасываемых цифр равна 5 и все значащие цифры, идущие за ней равны нулю, то последняя сохраняемая цифра увеличивается на 1, если она нечетная, и не изменяется, если она четная.
4. Погрешность суммы и разности приближенных чисел
Абсолютная погрешность алгебраической суммы или разности нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел:
;
.
Предельная абсолютная погрешность суммы или разности определяется следующим образом:
;
.
Оценим относительную погрешность 
суммы приближенных чисел. Пусть Х1 , Х2 - точные числа одного знака, х1 , х2 - их приближения. Тогда
£ 
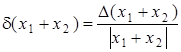(1)
где 
.
Предельная относительная погрешность суммы двух чисел вычисляется как
, (2)
где 
.
Формулы (1) и (2) можно обобщить на случай произвольного количества слагаемых:
Таким образом, при суммировании чисел одного знака не происходит потери относительной точности, что видно из приведенных соотношений.
Оценка относительной погрешности для разности двух чисел осуществляется по формуле
£ ndmax ,
Где
; 
.
Формулы для предельных относительных погрешностей имеют вид:
Очевидно, что для разности приближенных чисел относительные погрешности возрастают в n раз, где n > 1. При этом возможна существенная потеря точности, которая происходит в том случае, если числа X1 , X2 настолько близки, что их сумма значительно превышает их разность 
. Тогда n >> 1, что приводит к полной или почти полной потере точности. Такая ситуация называется катастрофической потерей точности.
5. Погрешности произведения и частного приближенных чисел
Формулы для оценки абсолютной погрешности произведения и частного является более сложными, чем для суммы и разности. Поэтому для частного и произведения абсолютные погрешности обычно определяют, используя известную формулу