Контрольная работа: Постановка и основные свойства транспортной задачи

если приращение стоимости продукта v_j – u_j меньше транспортных расходов c_ij , то такая перевозка убыточна, а потому . Если же приращение стоимости продукта v_j – u_j больше транспортных расходов c_ij (3.1.14), то эта перевозка прибыльна, а потому ее величина должна быть максимальной, т.е. .

Таким образом, теорема 3.3 по существу выражает принцип рентабельности для T_d – задачи.

Открытые транспортные модели. Существует ряд практических задач, в которых условие баланса не выполняется. Такие модели называются открытыми. Возможные два случая:

1)

2)

В первом случае полное удовлетворение спроса невозможно.

Такую задачу можно привести к обычной транспортной задаче следующим образом. Обозначим через величину штрафа из-за неудовлетворения запросов на единицу продукта в пункте B_j .

Тогда требуется минимизировать

(1.15)

при условиях

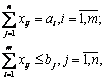
где - неудовлетворенный спрос.

Задачу (3.1.15) приводят к обычной Т-задаче введением фиктивного пункта производства А _m+1 , с объемом производства и транспортными издержками В таком случае Т-задача будет иметь вид

минимизировать

при условиях

В найденном решении х_опт полагаем все перевозки из фиктивного пункта А _m+1 равными нулю, т.е. .

Рассмотрим теперь второй случай. Введем фиктивный пункт B _n+1 с объемом спроса . Пусть - это убытки (штраф) в пункте А_і за единицу невывезенного продукта. Обозначим через сии_,n+1 = удельные транспортные издержки на перевозку единицы продукта с А _і в В _n+1 . Тогда соответствующая Т-задача запишется так:

минимизировать (1.16)

при условиях

(1.17) – (1.18)

В найденном решении все перевозки в фиктивный пункт В_n+1 считают равными нулю.

Опорные планы Т-задачи

Опорным (базисным) планом Т-задачи называют любое ее допустимое, базисное решение. Понятие опорного плана имеет наглядную геометрическую интерпретацию.

Последовательность коммуникаций

(1.19)

называют маршрутом, соединяющим пункты (рис. 2).

…

.

Рис. 2