Контрольная работа: Прямоугольный волновод

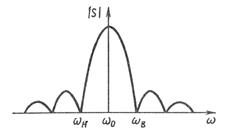
Рис. 5. Дисперсионная характеристика волновода

Чтобы найти плотность поверхностного электрического тока на идеально проводящих стенках волновода, следует воспользоваться следующей формулой [1](4.21)

Приведем выражения, определяющие пространственную зависимость комплексных амплитуд декартовых проекций векторов электромагнитного роля для волны типа Н₁₀ [1](8.52):

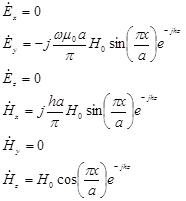(6)

Иногда бывает удобным несколько преобразовать систему равенств (6), выразив все комплексные амплитуды через -максимальную амплитуду напряженности электрического поля, наблюдаемую в центре широкой стенки волновода [1](8.53):

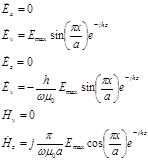(7)

Поскольку картина распределения силовых линий вектора в волне рассматриваемого типа известна, построение линий тока на стенках не представляет затруднений: эти линии образуют семейство кривых, ортогональных семейству силовых линий напряженности магнитного поля Рис.4.. Подчеркнем еще раз, что здесь изображена картина мгновенного распределения токов; во времени она перемещается вдоль оси волновода с фазовой скоростью.

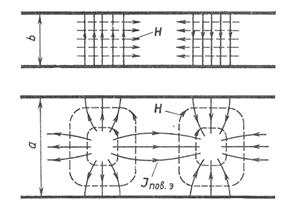
Рис. 6. Распределение векторов плотности поверхностного электрического тока на стенках прямоугольного волновода с волной типа Н₁₀

Картины распределения плотности поверхностного тока, соответствующего распределению поля этих типов волн на стенках волновода: [1] (стр.280 рис 10.10).

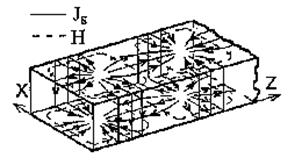
Рис. 7. Распределение векторов плотности поверхностного электрического тока на стенках прямоугольного волновода с волной типа Н₁₀

,

учитывая, что

находим

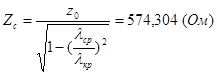Þ

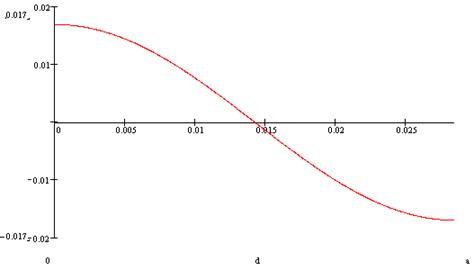
Рис. 8. Зависимость продольной составляющей Hz от поперечных координат x

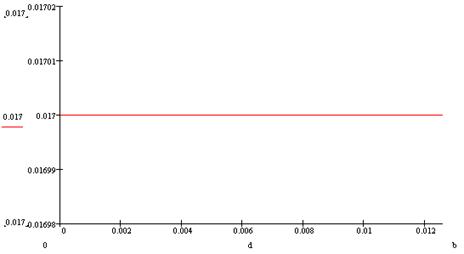
Рис. 9. Зависимость продольной составляющей Hz от поперечных координат y

Ez(x)=Ez(y)=0

Задание 3

Найдём центральную частоту рабочего диапазона:

, Þ.