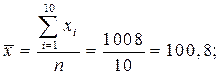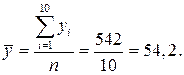Контрольная работа: Приклади рішення задач з економетрії

1128

3177,6

1587,4

26,6

819,6

Здесь средние значения переменных определяются из соотношений

Используя формулы, получим

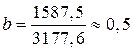a =54,2-0,5·100,8»3,8.

Окончательно, получим:

.

Количественная оценка параметра а=0,5 показывает, что среднее увеличение затрат при возрастании фондоемкости продукции на 1 усл.ед. составляет 0,5 усл.ед.

При построении эконометрической модели очень важным является вопрос о степени зависимости между регрессором и регрессантом, т.е. о тесноте связи между ними. Простейшим критерием, позволяющим получить количественную оценку влияния объясняющей переменной на объясняемую, является выборочный коэффициент корреляции (или просто коэффициент корреляции ). Он рассчитывается по следующей формуле:

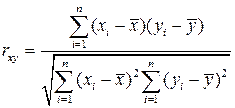
или, другая форма представления:

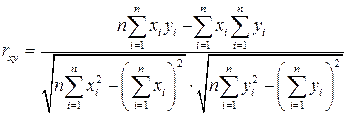
Из выражения видно, что коэффициент корреляции по абсолютной величине не превосходит единицу, т.е. -1 £ r_xy £ 1 . При этом, чем ближе |r_xy | к единице, тем теснее связь. При r_xy = ± 1 корреляционная связь представляет собой линейную функциональную зависимость, а наблюдаемые значения располагаются на прямой линии. Если r_xy =0, то считают, что корреляция отсутствует. Линия регрессии при этом параллельна оси абсцисс.

Принято считать, что связь между переменными высокая , если r_xy ³ 0,8, если 0,7 £ r_xy <0,8 , то связь считают средней , при 0,6 £ r_xy <0,7 - связь заметная , а в остальных случаях (r_xy <0,6) связь является низкой и следует пересмотреть выбор объясняющей переменной в рассматриваемом эконометрическом исследовании.

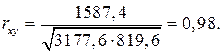
Коэффициент корреляции показывает, что связь между переменными в рассматриваемой задаче очень тесная.

3.4. Нелинейные модели

Простая регрессионная модель может быть нелинейна в двух смыслах:

1) регрессия не является линейной по объясняющей переменной, но линейна по оцениваемым параметрам;