Контрольная работа: Приклади рішення задач з економетрії

Нелинейность по переменным всегда можно обойти, используя замену переменных, например,

· выражение можно привести к линейному виду, используя подстановку:

Имеем линейное уравнение с тремя переменными :

.

Способ параметризации полученного многофакторного уравнения основывается на 1МНК и будет рассмотрен позднее.

· аналогично можно преобразовать квадратичною функцию y =а+ bx + c х² . Ее приводим к линейной с помощью замены: z ₁ = x , z ₂ = x ² . Получим:

y=a+bz₁ +cz₂ . (3.22)

Следует отметить, что найти параметры квадратичной функции y=ах² +bx+c можно и не используя линеаризацию (3.22). Осуществить параметризацию можно с помощью непосредственного применения МНК, при этом получим следующую систему нормальных уравнений (индексы суммирования опущены):

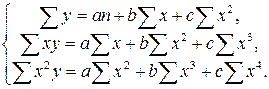(3.23)

Решить ее можно, например, с помощью метода Крамера (метода определителей).

Пример 3.2. Предполагается, что объем потребления некоторого товара имеет квадратичную зависимость от уровня дохода семьи в месяц (условные данные приведены в таблице). Требуется найти уравнение, выражающее эту зависимость.

Таблица 3.4

Доход семьи, грн.	800	1030	752	950	1004	837	986	1016	899	1005
Объем потребления товара, кг.	0,20	« 12 13 14 15 16 17 18 19 20 21 » К-во Просмотров: 656 Бесплатно скачать Контрольная работа: Приклади рішення задач з економетрії >>> Скачать <<< Меню Поиск