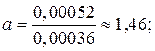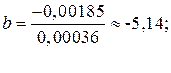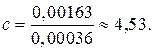Контрольная работа: Приклади рішення задач з економетрії

7,86

6,02

5,88

6,20

0,00

0,013

Данные полученные в таблице подставим в систему (3.23), получим

.

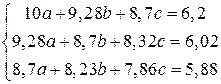Решая ее методом Крамера, имеем:

D=0,00036;

D1 =0,00052;

D2 =-0,00185;

D3 =0,00163.

Тогда,

Искомая модель имеет вид:

. (3.24)

Подставив последовательно в полученное уравнение (3.24) значения х _i , получим теоретические значения (столбец 9). Как видно из таблицы 3.5 теоретические значения регрессанта близки по своему значению к эмпирическим данным y_i , этот же факт подтверждают и малые значения остатков (столбец 10). Можно утверждать, что квадратичное уравнение (3.24) хорошо описывает рассматриваемый экономический процесс.

Проблема преобразования нелинейных по параметрам соотношений представляет особый интерес в эконометрических исследованиях. Этот класс нелинейных моделей можно подразделить на два типа[1] :

1) нелинейные модели внутренне линейные (те, которые с помощью элементарных преобразований можно свести к линейным);

2) нелинейные модели внутренне нелинейные (не могут быть сведены к линейным функциям).

К внутренне линейным можно отнести функции:

· степенную

· показательную

· экспоненциальную y=e^a+bx .

Перечисленные функции можно свести к линейным логарифмированием обеих частей выражения (обычно логарифмируют по основанию е ).

Для степенной функции получим:

(3.25)