Контрольная работа: Прогнозування моделями простої лінійної регресії
де ![]() - число збігів та незбігів знаків відхилень значень фактичної і результативної ознак від своїх середніх, тобто
- число збігів та незбігів знаків відхилень значень фактичної і результативної ознак від своїх середніх, тобто ![]() При цьому фіксуються збіги та незбіги знаків в відхиленнях від середньої у різних пар значень ознак.
При цьому фіксуються збіги та незбіги знаків в відхиленнях від середньої у різних пар значень ознак.
Коефіцієнт Фехнера К змінюється в межах від - 1 до +1. Якщо зв’язок між ознаками обернений, то К від’ємний; у випадку прямого зв’язку - додатній. Чим ближче К до ![]() , тим зв’язок більш тісний.
, тим зв’язок більш тісний.
Приклад 2. Розрахувати коефіцієнт Фехнера для наступних даних:
Таблиця 3
| Стаж роботи, х | Виробіток на 1 робітника, у | Збіг чи незбіг знаків | ||
| 2,5 | - | 222 | - | С |
| 2,5 | - | 223 | - | С |
| 1 | - | 200 | - | С |
| 1 | - | 202 | - | С |
| 1 | - | 205 | - | С |
| 5 | + | 244 | + | С |
| 5 | + | 250 | + | С |
| 3 | + | 234 | + | С |
| 4,5 | + | 241 | + | С |
| 4,5 | + | 244 | + | С |
| 2,7 | - | 230 | + | Н |
Коефіцієнт Фехнера
![]()
Величина К досить близька до величини коефіцієнта рангової кореляції Спірмена, що свідчить про тісний зв’язок між ознаками х і у .
3. Коефіцієнти асоціації і контингенції
Для визначення тісноти зв’язку двох якісних ознак, кожна із котрих складається тільки із двох груп, використовують коефіцієнти асоціації і контингенції. Для їх розрахунку будується чотирьохклітинна таблиця кореляції, котра виражає зв’язок між двома явищами, кожне із них в свою чергу повинно бути альтернативним, тобто складається із двох якісно відмінних друг від друга значень ознаки (наприклад, хороший, поганий).
Наприклад, при вивчені залежності врожайності від кількості внесених в ґрунт добрив виділимо по врожайності і по кількості внесених добрив лише по дві групи. При цій умові можна побудувати наступну чотирьохклітинну таблицю.
Таблиця 4
|
Удобрено Урожайність | Добре | Погано | Всього |
| Висока | а | в | a+b |
| Низька | с | d | c+d |
| Всього | а+c | b+d |
Числа, які стоять на перетині рядків і граф a, в, c, d показують, скільки дільниць зустрічаються з тою або другою кількістю добрив, що внесені в ґрунт, з тією або другою врожайністю.
Коефіцієнт асоціації Юла і коефіцієнт контингенції розраховується за наступними формулами:
асоціації Юла![]() ;
;
контингенції 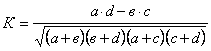 .
.
де a, в, c, d - кількісні характеристики досліджувальних груп.
Коефіцієнт контингенції завжди менший коефіцієнта асоціації Юла. Зв’язок рахується підтвердженим, якщо:
![]() або
або ![]() .
.
Приклад 3. Дослідити зв’язок між виконанням норм виробітку молодими робітниками і закінченням ними середньої школи. Результати обстеження характеризуються даними (табл. 5).
Таблиця 5
| Групи робітників | Виконують норму | Не виконують норму | Всього |
| Закінчили середню школу | 78 | 22 | 100 |
| Не закінчили середню школу | 32 | 68 | 100 |
| Всього | 110 | 90 | 200 |
Рішення. За даними таблиці
![]()
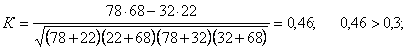
Між досліджувальними ознаками спостерігається чіткий зв’язок, що підтверджується досить високими значеннями коефіцієнтів асоціації і контингенції.
4. Коефіцієнт взаємної спряженості Пірсона і Чупрова
Якщо кожна із якісних ознак складається більше ніж із двох груп, то для визначення тісноти зв’язку можна використати коефіцієнт взаємної спряженості Пірсона. Цей коефіцієнт розраховується за наступною формулою:
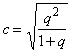
де q2 - показник взаємної спряженості.
Коефіцієнт Чупрова: