Контрольная работа: Прогнозування моделями простої лінійної регресії

НЕПАРАМЕТРИЧНІ МЕТОДИ ОЦІНКИ ТІСНОТИ ЗВ`ЯЗКУ

План

1. Критерії Спірмена та Кендала

2. Критерій Фехнера

3. Коефіцієнти асоціації і контингенції

4. Коефіцієнт взаємної спряженості Пірсона і Чупрова

Література

1. Критерії Спірмена та Кендала

Серед непараметричних (емпіричних) методів оцінки тісноти зв’язку найбільше значення мають розрахунки рангових коефіцієнтів Спірмена і Кендала .

Ці коефіцієнти можуть бути використанні для визначення тісноти зв’язку як між кількісними, так і між якісними ознаками при умові, якщо значення цих показників можуть бути впорядковані або проранговані по спаданню або зростанню ознаки.

Для визначення рангового коефіцієнта кореляції рангують (тобто записують у зростаючому або спадаючому порядку) всі значення факторної ознаки і разом з тим записують відповідні значення результативної ознаки . Другими словами, визначають ранг по обох ознаках, тобто номер кожної ознаки в рангових рядах.

Ступінь тісноти зв’язку між ознаками визначається ранговим коефіцієнтом кореляції Спірмена по формулі:

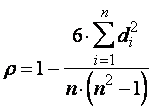
де - квадрати різниць рангів зв’язаних величин і ; п - число спостережень (число пар рангів).

У випадку відсутності зв’язку ; при прямому зв’язку коефіцієнт додатній, а при оберненому зв’язку - від’ємний.

Приклад 1. Визначити, чи існує залежність між стажем роботи та виробітком робітника для слідуючих даних:

Таблиця 1

№ п/п	Стаж роботи робітників, х, роки	Виробіток на 1 робітника, у
1	2,5	222
2	2,5	223
3	1	200
4	1	202
5	1	205
6	5	244
7	5	250
8	3	234
9	4,5	241
10	4,4	244
11	2,7	230

Рішення.

Фактори і ранжуємо (впорядкуємо) в порядку зростання (спадання) їх значень і заповнюємо табл. 2.

Таблиця 2

		Ранг ознаки х	Ранг ознаки у	Рангова різниця
1	200	4	3	1	1
1	202	4	4	0	0
1	205	4	5	-1	1
2,5	222	1,5	1	0,5	0,25
2,5	223	1,5	2	-0,5	0,25
2,7	230	11	11	0	0
3	234	8	8	0	0
4,4	241	10	9	1	1
4,5	244	9	8	1	1
5	244	6,5	8	-1,5	2,25
5	250	6,5	7	-0,5	0,25
Всього				3,5-3,5=0	7

Визначаємо ранги по обох ознаках, тобто номер кожної ознаки в рангованих рядах. Для рівних значень факторів х та у ранг знаходять шляхом ділення суми рангів, що приходяться на неї, на число рівних значень.

3. Знаходимо рангову різницю та.

4. Розрахуємо коефіцієнт кореляції рангів Спірмена:

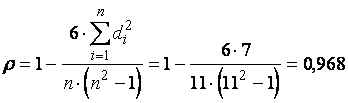
Розрахунок рангового коефіцієнта Кендала відбувається за формулою:

де п - число спостережень; S - сума додатних та від’ємних балів по одній із зв’язаних величин, ранги котрої розміщені у відповідності з впорядкованими рангами другої.

2. Критерій Фехнера

Одним із найпростіших показників кореляційної залежності, пов’язаний з іменем відомого німецького вченого психофізика Фехнера.

Коефіцієнт Фехнера базується на застосуванні перших ступенів відхилень всіх значень взаємозв’язаних ознак від середньої величини по кожній ознаці.

Коефіцієнт Фехнера вимірює тісноту зв’язку за наступною формулою:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--