Контрольная работа: Проходження світла через кристали та нелінійні оптичні явища

Оптичні середовища, показник заломлення яких залежить від напряму поширення світлової хвилі, називають анізотропними або кристалічними.

Анізотропія кристалів зумовлена симетрією їх внутрішнього стану. В ізотропному середовищі при впливі електричного поля виникає зміщення електричних зарядів, що характеризується вектором електричного зміщення , причому вектори і колінеарні і пов'язані рівнянням (1).

В анізотропному середовищі в загальному випадку електричні заряди зміщуються не у напрямі прикладеного електричного поля і вектори не співпадають ні по модулю, ні у напрямі.

Однак в будь-якому кристалі існують три головних напрями, для яких зберігається колінеарність векторів і і справедливі співвідношення:

; ; , (1)

причому осі координат , , вибрані вздовж головних напрямів. У загальному випадку (рис. 1. а).

У вибраній системі координат , , для будь-якого кристала

Рис. 1 Проходження світла через кристали

Головні напрями можна записати рівняння так званої характеристичної поверхні:

,

де , , - головні показники заломлення.

Характеристична поверхня являє собою еліпсоїд Френеля, причому довжини головних напівосей цього еліпсоїда рівні відповідно (), () і () (рис. 1 б).

З аналітичної геометрії відомо, що будь-який еліпсоїд має два кругових перетини.

Напрями, що перпендикулярні круговим перетинам еліпсоїда Френеля, називають оптичними осями кристала. Отже, кристал у загальному випадку має дві оптичні осі (двовісний кристал). Якщо , то еліпсоїд Френеля вироджується в еліпсоїд обертання, що характеризує одновісний кристал з оптичною віссю вздовж осі .

Будь-яку площину, проведену через оптичну вісь, називають головним перетином кристала.

При поширенні світлових хвиль в анізотропному середовищі з напрямом коливань вздовж головних напрямів , , фазові швидкості мають той же напрям, що і вектор . У цьому випадку на основі (1) отримаємо

; ; .

Однак при довільному напрямі коливань вектор фазової швидкості хвилі неколінеарний вектору , що характеризує також напрям світлового променя і групової швидкості хвилі.

Нехай лінійно поляризована плоска світлова хвиля розповсюджується вздовж осі , причому вектор складає кут з віссю (рис. 2).

Розкладемо початкове коливання на дві що складають, одна з яких має напрям вздовж осі , а інша – вздовж осі . Таким чином, в кристалі вздовж осі розповсюджуються дві хвилі з різними фазовими швидкостями і . На виході кристала між цими хвилями виникає різниця фаз

,

де – товщина кристала.

У залежності від значення між двома хвилями виникає різниця фаз , що в загальному випадку призводить до еліптичної поляризації.

При , де , і виконуються умови виникнення кругової поляризації, і лише при зберігається лінійна поляризація світлової хвилі.

В анізотропних середовищах має місце подвійне променезаломлення. Пояснимо це явище на прикладі одноосного кристала. Нехай з повітря на кристал під кутом падає пучок неполяризованого світла, причому для даного кристала і оптична вісь направлена по осі . Визначимо , а .

Розкладемо падаючу хвилю на дві, що складають, в одній з яких вектор коливається вздовж осі , а в іншій – в площині . Для цих хвиль на основі закону заломлення можна написати такі співвідношення:

;

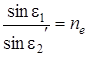--> ЧИТАТЬ ПОЛНОСТЬЮ <--