Контрольная работа: Работа с массивами и решение систем уравнений в Mathcad

stack(M1,M2)

объединяет в одну две матрицы, имеющие одинаковое число столбцов, располагая М1 над М2

submatrix(A,ir,jr,ic,jc)

возвращает субматрицу, состоящую из всех элементов содержащихся в строках от ir по jr и столбцов с ic по jc (ir£jr и ic£jc)

diag(V)

создает диагональную матрицу, элементы главной диагонали которой равны элементам вектора V

matrix(m,n,f)

создает матрицу, в которой (i, j) элемент равен f(i,j), где i=0, 1, …, m и j=0, 1, …, n; f(i,j) - некоторая функция

cols(M)

возвращает число столбцов матрицы M

rows(M)

возвращает число строк матрицы M

rank(M)

возвращает ранг матрицы M

tr(M)

возвращает след (сумму диагональных элементов) матрицы M

mean(M)

возвращает среднее значение элементов матрицы M

Примеры работы с матрицами приведены на рисунке 2.2.

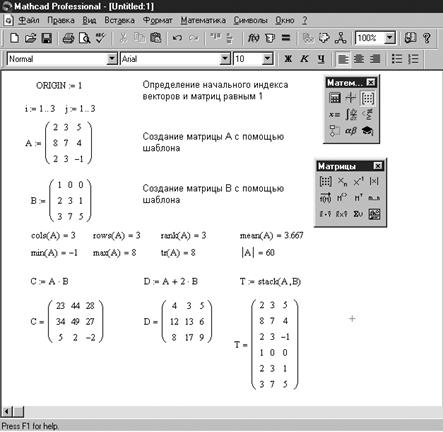
Рис. 2.2. Примеры работы с матрицами

3. Решение систем линейных уравнений

Векторные и матричные операторы и функции позволяют решать широкий круг задач линейной алгебры.

Например, если задана матрица A и вектор B для системы линейных уравнений в матричной форме , то вектор решения X можно получить из уравнения .

Поскольку решение систем линейных уравнений довольно распространенная задача, то в Mathcad введена специальная функция lsolve(A,B) , которая возвращает вектор X для системы линейных уравнений при заданной матрице коэффициентов A и векторе свободных членов B. Если уравнений n, то размер вектора B должен быть n, а матрицы A - n´n.

Пусть необходимо решить систему уравнений

.

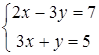В нашем случае матрицы A и B определяется следующим образом: