Контрольная работа: Растворение твердых веществ
 (18)
(18)
где ![]() - время, необходимое для достижения любого значения
- время, необходимое для достижения любого значения ![]() в условиях периодического опыта, т.е. при переменной концентрации активного реагента
в условиях периодического опыта, т.е. при переменной концентрации активного реагента ![]() .
.
Верхние пределы интегрирования  и
и 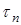 выражают соответственно время, необходимое для достижения определенного значения
выражают соответственно время, необходимое для достижения определенного значения  и время полного растворения в периодическом опыте с изменяющейся концентрацией реагента (в отличие от
и время полного растворения в периодическом опыте с изменяющейся концентрацией реагента (в отличие от  и
и 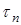 , выражающих те же понятия, но при постоянной концентрации С.
, выражающих те же понятия, но при постоянной концентрации С.
2. По уравнению (18) вычисляют значение х, отвечающее определенному значению ![]() .
.
При этом верхний предел интеграла, стоящий в числителе, означает время необходимое для достижения этого значения ![]() в периодическом опыте. Такие вычисления проводят для ряда последовательных значений доли нерастворившегося компонента
в периодическом опыте. Такие вычисления проводят для ряда последовательных значений доли нерастворившегося компонента ![]() . Результаты расчетов, представленные в виде графика, таблицы или апроксимированные аналитическим выражением, дают кинетическую функцию
. Результаты расчетов, представленные в виде графика, таблицы или апроксимированные аналитическим выражением, дают кинетическую функцию ![]()
Графический вариант описанного метода иллюстрируется рис.1

Рис.1. К графическому определению кинетической функции
Значение х соответствующее некоторому ![]() , равно отношению заштрихованной площади ко всей площади под кривой
, равно отношению заштрихованной площади ко всей площади под кривой ![]() . С помощью такого графика можно легко определить значение х для ряда значений
. С помощью такого графика можно легко определить значение х для ряда значений ![]() и составить таблицу или построить график зависимости
и составить таблицу или построить график зависимости ![]() .
.
Из уравнения (18) видно, что для определения х нужно знать зависимость скорости процесса от концентрации, т.е. функцию  .
.
Если, например  , то должен быть известен порядок реакции
, то должен быть известен порядок реакции  . Тогда уравнение (18) принимает вид:
. Тогда уравнение (18) принимает вид:
 (19)
(19)
Входящие в уравнение (18) и (19) интегралы могут быть определены численными или графическими методами. Необходимая для выполнения интегрирования зависимость ![]() от
от ![]() , а также связь между
, а также связь между ![]() и
и ![]() , содержатся в результатах периодического опыта.
, содержатся в результатах периодического опыта.
Таким образом, уравнение (18) позволяет вычислить значения, отвечающие любому значению ![]() , и тем самым определить кинетическую функцию.
, и тем самым определить кинетическую функцию.
2.4 Определение времени полного растворения
В отличие от кинетической функции  , которая сохраняет свой вид для любых постоянных значений Т и С, величина
, которая сохраняет свой вид для любых постоянных значений Т и С, величина  всегда относится к совершенно определенным условиям растворения и изменяется при изменении этих условий. Очевидно, что если растворение проходит при постоянной концентрации активного реагента, то величина
всегда относится к совершенно определенным условиям растворения и изменяется при изменении этих условий. Очевидно, что если растворение проходит при постоянной концентрации активного реагента, то величина  совпадает со временем полного растворения в периодическом опыте:
совпадает со временем полного растворения в периодическом опыте:  . При переменной концентрации дело обстоит иначе: величина
. При переменной концентрации дело обстоит иначе: величина  связана с
связана с 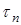 отношением:
отношением:
 (20)
(20)
В частности, для определения времени полного растворения при некоторых фиксированных значениях ![]() и
и ![]() достаточно подставить в уравнение (20)
достаточно подставить в уравнение (20) ![]() вместо
вместо ![]() и
и ![]() вместо
вместо ![]() :
:
 (21)
(21)
Естественно использовать для определения ![]() тот периодический опыт, для которого
тот периодический опыт, для которого ![]() . Тогда формула (21) упрощается:
. Тогда формула (21) упрощается:
 (22)
(22)
Входящий в уравнения (21) и (22) интеграл численно равен площади под кривой ![]() на рис.1. Для его вычисления можно воспользоваться любым из известных методов.
на рис.1. Для его вычисления можно воспользоваться любым из известных методов.
Таким образом, результаты периодического опыта, проведенного при изменяющейся концентрации активного реагента ![]() , позволяют легко определить время полного растворения
, позволяют легко определить время полного растворения ![]() , относящейся к постоянным значениям
, относящейся к постоянным значениям ![]() и
и ![]() . Для перехода к иным значениям концентрации и температуры можно воспользоваться соотношением, вытекающим из уравнений (20) и (21).
. Для перехода к иным значениям концентрации и температуры можно воспользоваться соотношением, вытекающим из уравнений (20) и (21).
 (23)
(23)
В частности, если ![]() и
и ![]() , то:
, то:
 (24)
(24)
Таким образом, зная энергию активации Е, порядок реакции ![]() и время полного растворения
и время полного растворения ![]() при некоторых фиксированных значениях
при некоторых фиксированных значениях ![]() и
и ![]() по формуле (24) можно вычислить время полного растворения
по формуле (24) можно вычислить время полного растворения ![]() при любых значениях
при любых значениях ![]() и
и ![]() .
.
2.5 Рекомендации по проведению исследований и выполнению расчетов
Результаты одного лабораторного периодического опыта в принципе позволяют определить кинетическую функцию ![]() . В действительности нужно провести серию опытов в диапазоне интересующих значений концентрации активного реагента и температуры. Это необходимо для обеспечения надежности кинетических величин.
. В действительности нужно провести серию опытов в диапазоне интересующих значений концентрации активного реагента и температуры. Это необходимо для обеспечения надежности кинетических величин.
Кроме того, проведение серии опытов необходимо для экспериментального подтверждения инвариантности кинетической функции относительно концентрации и температуры.
Результатом такой серии опытов будет совокупность кривых ![]() . Из каждой кривой нужно определить кинетическую функцию, вычислив для ряда значений
. Из каждой кривой нужно определить кинетическую функцию, вычислив для ряда значений ![]() соответствующие значения х по формуле (18). Из этой формулы следует, что для расчета нужно знать время полного растворения
соответствующие значения х по формуле (18). Из этой формулы следует, что для расчета нужно знать время полного растворения ![]() в периодическом опыте и иметь достаточно надежные данные о ходе кинетической кривой во всем диапазоне значений
в периодическом опыте и иметь достаточно надежные данные о ходе кинетической кривой во всем диапазоне значений ![]() от 0 до
от 0 до ![]() .
.
Аргумент кинетической функции х есть отношение продолжительности растворения  и времени полного растворения
и времени полного растворения  . Величина
. Величина  играет, следовательно, роль нормировочного множителя или масштабного коэффициента, позволяющего выразить время в безразмерных единицах. В качестве такого коэффициента с равным успехом может быть использовано время, необходимое для достижения любого фиксированного значения
играет, следовательно, роль нормировочного множителя или масштабного коэффициента, позволяющего выразить время в безразмерных единицах. В качестве такого коэффициента с равным успехом может быть использовано время, необходимое для достижения любого фиксированного значения  . Пусть это фиксированное значение равно
. Пусть это фиксированное значение равно  , оно должно быть выбрано таким образом, чтобы изменению
, оно должно быть выбрано таким образом, чтобы изменению  от 1 до
от 1 до  соответствовали достаточно надежные участки всех экспериментальных кривых. Время, необходимое для достижения значения
соответствовали достаточно надежные участки всех экспериментальных кривых. Время, необходимое для достижения значения  при постоянных температуре и концентрации активного реагента, обозначим через
при постоянных температуре и концентрации активного реагента, обозначим через  . Введем теперь новое безразмерное время
. Введем теперь новое безразмерное время  :
:  . При обработке экспериментальных данных относящихся к каждому проведенному опыту, вместо определения х по формуле (18) вычисляют значения
. При обработке экспериментальных данных относящихся к каждому проведенному опыту, вместо определения х по формуле (18) вычисляют значения  по формуле:
по формуле:
 (25)
(25)
где ![]() -время, необходимое для достижения
-время, необходимое для достижения ![]() в периодическом опыте.
в периодическом опыте.