Контрольная работа: Решение линейной системы уравнений с тремя неизвестными

3) Исследуем функцию на экстремумы и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:

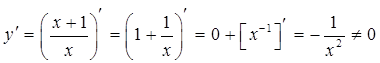
Следовательно, функция не имеет критических точек первого рода.

Так как y’ < 0 для всех х, то функция убывает во всей области определения

4) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:

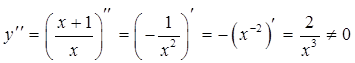
Итак функция не имеет точек перегиба. Разобьем область определения точкой х = 1 в каждой из которых установим знак второй производной:

х	(-¥; 0)	0	(0; ¥)
f ‘’(x)	-	не существует	+
f(x)	Ç	не существует	È

5) Выясним наличие у графика заданной функции асимптот. Для определения параметров уравнения асимптоты y = kx + b воспользуемся формулами

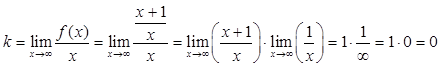
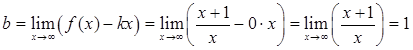
Таким образом, у графика заданной функции есть наклонная асимптота

y = 0*x + 1 = 1.

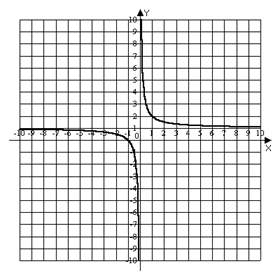
6) построим график функции